Contents

Final Project NBA Players

Final Project NBA Players

Author: Rex Kim

Course Project Preparation, UC Irvine, Math 10, W22

Introduction

This project dives into advanced statistics of current NBA players in the 2021-2022 NBA season. Different statistical categories include win shares (WS), value over replacement player (VORP), and box plus/minus. I’m going to discover how the NBA ranks its top 10 current NBA players based on the categories just listed as well as other main stats such as points, rebounds, and assists.

Main portion of the project

(You can either have all one section or divide into multiple sections)

import seaborn as sns
import numpy as np
import pandas as pd
import altair as alt
import matplotlib as mpl
import matplotlib.pyplot as plt

from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import log_loss


df = pd.read_csv('nba_2020_adv.csv')
df
Player Pos Age Tm G MP PER TS% 3PAr FTr ... TOV% USG% OWS DWS WS WS/48 OBPM DBPM BPM VORP
0 Steven Adams C 26 OKC 63 1680 20.5 0.604 0.006 0.421 ... 14.2 17.3 3.8 2.7 6.5 0.185 1.9 1.1 2.9 2.1
1 Bam Adebayo PF 22 MIA 72 2417 20.3 0.598 0.018 0.484 ... 17.6 21.2 4.6 3.9 8.5 0.168 1.4 2.0 3.4 3.3
2 LaMarcus Aldridge C 34 SAS 53 1754 19.7 0.571 0.198 0.241 ... 7.8 23.4 3.0 1.4 4.5 0.122 1.8 -0.5 1.4 1.5
3 Kyle Alexander PF 23 MIA 2 13 4.7 0.500 0.000 0.000 ... 33.3 10.2 0.0 0.0 0.0 -0.003 -6.1 -3.5 -9.6 0.0
4 Nickeil Alexander-Walker SG 21 NOP 47 591 8.9 0.473 0.500 0.139 ... 16.1 23.3 -0.7 0.4 -0.2 -0.020 -3.2 -1.4 -4.6 -0.4
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
646 Trae Young PG 21 ATL 60 2120 23.9 0.595 0.455 0.448 ... 16.2 34.9 5.3 0.6 5.9 0.133 6.2 -2.3 3.9 3.1
647 Cody Zeller C 27 CHO 58 1341 18.8 0.576 0.157 0.374 ... 11.9 20.8 2.3 1.3 3.6 0.129 0.2 -0.8 -0.6 0.5
648 Tyler Zeller C 30 SAS 2 4 22.4 0.250 0.000 0.000 ... 0.0 43.2 0.0 0.0 0.0 -0.075 -0.3 -22.1 -22.4 0.0
649 Ante Žižić C 23 CLE 22 221 16.4 0.597 0.000 0.264 ... 11.1 17.5 0.3 0.2 0.5 0.106 -1.7 -1.5 -3.2 -0.1
650 Ivica Zubac C 22 LAC 72 1326 21.7 0.651 0.005 0.431 ... 11.8 16.4 4.4 2.3 6.6 0.241 1.9 0.8 2.8 1.6

651 rows × 26 columns

I will locate all players in the NBA and the position they play.

df.loc[:,["Player","Pos"]]
Player Pos
0 Steven Adams C
1 Bam Adebayo PF
2 LaMarcus Aldridge C
3 Kyle Alexander PF
4 Nickeil Alexander-Walker SG
... ... ...
646 Trae Young PG
647 Cody Zeller C
648 Tyler Zeller C
649 Ante Žižić C
650 Ivica Zubac C

651 rows × 2 columns

Because how much popularized the point guard position is, I decided to check all point guards and their statistics.

df.loc[df['Pos'] == 'PG']
Player Pos Age Tm G MP PER TS% 3PAr FTr ... TOV% USG% OWS DWS WS WS/48 OBPM DBPM BPM VORP
17 Ryan Arcidiacono PG 25 CHI 58 930 9.0 0.551 0.627 0.173 ... 13.5 12.5 0.7 0.7 1.4 0.071 -2.7 -0.1 -2.8 -0.2
21 D.J. Augustin PG 32 ORL 57 1420 14.0 0.554 0.436 0.393 ... 13.7 19.1 2.0 0.9 2.9 0.098 -0.3 -1.3 -1.6 0.2
25 Lonzo Ball PG 22 NOP 63 2025 13.1 0.517 0.575 0.111 ... 21.1 18.5 0.4 2.0 2.4 0.058 0.1 0.6 0.6 1.3
27 J.J. Barea PG 35 DAL 29 450 14.6 0.512 0.411 0.106 ... 14.9 24.2 0.5 0.2 0.7 0.072 1.6 -3.0 -1.4 0.1
53 Patrick Beverley PG 31 LAC 51 1342 12.5 0.560 0.604 0.138 ... 15.4 13.3 1.6 2.0 3.6 0.128 -0.3 2.5 2.2 1.4
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
618 Tremont Waters PG 22 BOS 11 119 4.3 0.381 0.490 0.163 ... 22.2 24.2 -0.5 0.2 -0.3 -0.103 -8.5 1.0 -7.5 -0.2
623 Russell Westbrook PG 31 HOU 57 2049 21.0 0.536 0.166 0.297 ... 15.0 34.4 1.7 2.5 4.2 0.098 1.6 -0.1 1.5 1.8
638 Nigel Williams-Goss PG 25 UTA 10 50 8.1 0.415 0.438 0.125 ... 15.1 17.4 -0.1 0.1 0.0 0.017 -5.2 1.3 -3.9 0.0
644 Justin Wright-Foreman PG 22 UTA 4 45 8.8 0.437 0.500 0.200 ... 12.1 24.1 -0.1 0.1 0.0 -0.008 -7.0 -2.0 -9.0 -0.1
646 Trae Young PG 21 ATL 60 2120 23.9 0.595 0.455 0.448 ... 16.2 34.9 5.3 0.6 5.9 0.133 6.2 -2.3 3.9 3.1

111 rows × 26 columns

df.loc[df['Pos'] == 'PG']
Player Pos Age Tm G MP PER TS% 3PAr FTr ... TOV% USG% OWS DWS WS WS/48 OBPM DBPM BPM VORP
17 Ryan Arcidiacono PG 25 CHI 58 930 9.0 0.551 0.627 0.173 ... 13.5 12.5 0.7 0.7 1.4 0.071 -2.7 -0.1 -2.8 -0.2
21 D.J. Augustin PG 32 ORL 57 1420 14.0 0.554 0.436 0.393 ... 13.7 19.1 2.0 0.9 2.9 0.098 -0.3 -1.3 -1.6 0.2
25 Lonzo Ball PG 22 NOP 63 2025 13.1 0.517 0.575 0.111 ... 21.1 18.5 0.4 2.0 2.4 0.058 0.1 0.6 0.6 1.3
27 J.J. Barea PG 35 DAL 29 450 14.6 0.512 0.411 0.106 ... 14.9 24.2 0.5 0.2 0.7 0.072 1.6 -3.0 -1.4 0.1
53 Patrick Beverley PG 31 LAC 51 1342 12.5 0.560 0.604 0.138 ... 15.4 13.3 1.6 2.0 3.6 0.128 -0.3 2.5 2.2 1.4
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
618 Tremont Waters PG 22 BOS 11 119 4.3 0.381 0.490 0.163 ... 22.2 24.2 -0.5 0.2 -0.3 -0.103 -8.5 1.0 -7.5 -0.2
623 Russell Westbrook PG 31 HOU 57 2049 21.0 0.536 0.166 0.297 ... 15.0 34.4 1.7 2.5 4.2 0.098 1.6 -0.1 1.5 1.8
638 Nigel Williams-Goss PG 25 UTA 10 50 8.1 0.415 0.438 0.125 ... 15.1 17.4 -0.1 0.1 0.0 0.017 -5.2 1.3 -3.9 0.0
644 Justin Wright-Foreman PG 22 UTA 4 45 8.8 0.437 0.500 0.200 ... 12.1 24.1 -0.1 0.1 0.0 -0.008 -7.0 -2.0 -9.0 -0.1
646 Trae Young PG 21 ATL 60 2120 23.9 0.595 0.455 0.448 ... 16.2 34.9 5.3 0.6 5.9 0.133 6.2 -2.3 3.9 3.1

111 rows × 26 columns

The following assigns a standard scaler to scaler and also initializes our training and testing data.

scaler = StandardScaler()
df[["BPM","USG%"]] = scaler.fit_transform(df[["BPM","USG%"]])

X_train, X_test, y_train, y_test = train_test_split(df[["BPM","USG%"]], df["Age"], test_size=0.2)

X = df[['USG%', 'BPM']]
X
USG% BPM
0 -0.179574 1.124504
1 0.512894 1.244773
2 0.903518 0.763698
3 -1.440223 -1.882216
4 0.885762 -0.679528
... ... ...
646 2.945413 1.365042
647 0.441872 0.282622
648 4.419128 -4.961097
649 -0.144063 -0.342775
650 -0.339375 1.100450

651 rows × 2 columns

Below, I’m ensuring that the dataframe X which holds usage rate and box plus/minus are resized for distribution.

scaler = StandardScaler()
scaler.fit(X)
X_scaled = scaler.transform(X)

y = df['Age']
y

0      26
1      22
2      34
3      23
4      21
       ..
646    21
647    27
648    30
649    23
650    22
Name: Age, Length: 651, dtype: int64

y_test

69     27
243    26
281    23
245    33
388    33
       ..
228    21
450    28
638    25
221    28
327    32
Name: Age, Length: 131, dtype: int64

The K-neighbors classifier is assigned to clf and this is where we create an Altair scatter plot with box plus/minus being on the x-axis and usage rate being on the y axis. I am also configuring the orientiation of the legend.

The Altair chart below shows when nearest neighbors has a k value of 1 meaning that the bias is 0. If k = 1, then the object is simply assigned to the class of that single nearest neighbor. By hovering over the rightmost players, we can see that the more notable players like James Harden and Lebron James lead the lead in box plus/minus but there are also players who played minimal minutes but had productive games.

clf = KNeighborsClassifier(n_neighbors=1)
clf.fit(X_train, y_train)
df["pred"] = clf.predict(df[["BPM","USG%"]])
c = alt.Chart(df).mark_circle().encode(
    x="BPM",
    y="USG%",
    color=alt.Color("pred", title="Age"),
    tooltip = ('Player:N','Age:Q','BPM:Q','USG%:Q','MP:Q')
).properties(
    title="Box Plus/Minus vs. Usage",
    width=1000,
    height=400,
)

c.configure_legend(
    strokeColor='gray',
    fillColor='#EEEEEE',
    padding=10,
    cornerRadius=10,
    orient='top-right'
)
alt.data_transformers.disable_max_rows()
print(f"The number of rows in this dataset is {df.shape[0]}")
c

The number of rows in this dataset is 651

Below I am checking to see whether there is overfitting or underfitting.

clf.score(X_train,y_train)

0.9903846153846154

clf.score(X_test,y_test)

0.08396946564885496

The data looks to be underfitting since the training set is lower than the testing set.

Here, I am creating another ten Altair scatter plots but when k neighbors increments from 1 to 9. Larger values of k will have smoother decision boundaries which mean lower variance but increased bias. In turn, this can significantly influence our result.

def make_chart(k):
    clf = KNeighborsClassifier(n_neighbors=k)
    clf.fit(X_train, y_train)
    df[f"pred{k}"] = clf.predict(df[["BPM","USG%"]])
    test_score = clf.score(X_test,y_test) 
    train_score = clf.score(X_train,y_train)
    c = alt.Chart(df).mark_circle().encode(
        x="BPM",
        y="USG%",
        color=alt.Color(f"pred{k}", title="Predicted Age"),
        tooltip = ('Player:N','Age:Q','BPM:Q','USG%:Q','MP:Q')
    ).properties(
        title=f"n_neighbors = {k}",
        width=1000,
        height=200,
    )
    c.configure_legend(
    strokeColor='gray',
    fillColor='#EEEEEE',
    padding=10,
    cornerRadius=10,
    orient='top-right'
)
    
    return c 

alt.vconcat(*[make_chart(k) for k in range(1,10)])

Below I will now attempt to create a boxplot for all players’ age, box plus/minus, and usage rate. I will include how to read a boxplot

Minimum: Smallest number in the dataset. First quartile: Middle number between the minimum and the median. Second quartile (Median): Middle number of the (sorted) dataset. Third quartile: Middle number between median and maximum. Maximum: Highest number in the dataset.

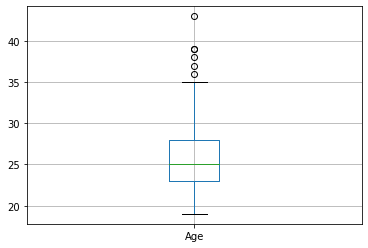
The boxplot below shows that the average age of NBA players is roughly 25 years. With outliers like Jamal Crawford being age 43.

ageBoxPlot = df.boxplot(column=['Age'])
../../_images/RexKim_28_0.png

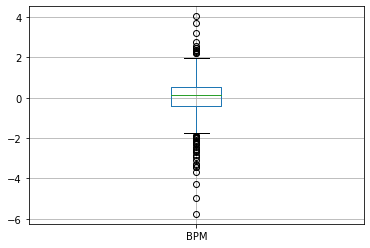
The boxplot below measures all NBA players box plus/minus. The lower the box plus/minus the lesser the player actually performs in game and contributes to winning. This isn’t exactly the best representation of NBA players as Jamal Crawford only played 6 total minutes this recorded season.

bpmBoxPlot = df.boxplot(column=['BPM'])
../../_images/RexKim_30_0.png

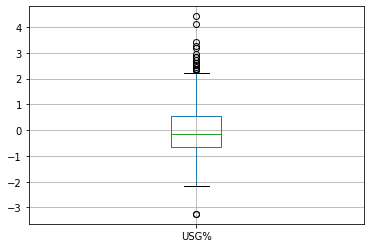
As k gets larger, there is lower variance and greater bias. This is how players like Tyler Zeller have such high usage rates despite playing such little minutes.

usgBoxPlot = df.boxplot(column=["USG%"])
../../_images/RexKim_32_0.png 
boxplot = df.boxplot(column=["Age","BPM","USG%"])
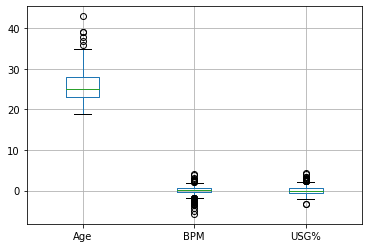
../../_images/RexKim_33_0.png

I found that specifying age, BPM, and USG% by position and top 10 players in the NBA was somewhat difficult. The plots and altair charts above represent the idea that there are only a select few players whose advanced statistics still remain high despite aging. Players like Stephen Curry, Kevin Durant, and Lebron James are namely a few.

Summary

In the NBA, win shares are calculated using main stats. In this project, I tried to determine if a player’s age of could be predicted by a player’s usage rate(USG%) and box plus/minus. The models above show that with increased age, majority of players’ USG% and BPM decrease significantly.

References

Include references that you found helpful. Also say where you found the dataset you used.

Information on pie charts and box plots https://deepnote.com/@a11s/Data-Visualisation-with-Python-EgfTyjpfS129FYXEnB2U7Q

URL to dataset https://www.kaggle.com/nicklauskim/nba-per-game-stats-201920

Created in deepnote.com Created in Deepnote

previous

Diamond price

next

Russian Federation Economic Indicators