Contents

Analysis of the Alcohol Drinking in UCI Student

Analysis of the Alcohol Drinking in UCI Student

Author: Jingxi.Feng (30294115)

Course Project, UC Irvine, Math 10, S22

Introduction

Introduce your project here. Maybe 3 sentences.

The dataset that I am using is actually realistic data from my another current class: Stastic 7. In that class, we learn about method of different kind of stastic testing and concluding any hypothesis base on the test result. The overlapping knowledge between stastic class and math 10 lead me to wonder if I would apply my knowledge from Math 10 to Stastic 7. In general, this dataset come from my project of creating survey and getting test statstic. My purpose of the Stastic 7 project is meant to find out drinking motivation, drinking frequence amount the studnet in UCI. In the help of the professor, I successfully collect 314 students information and prepare to conduct my hypothesis using Math 10 sills.

In the end, I will also introduce an extra dataset from Duke Univesity in order to do comparison.

Main portion of the project

Section 1: General Look of the Dataset

Section 2: Drinking level

Section 3: Descriptive Statistics in Drinking level

Section 4: Drinking Frequence

Section 5: Inferential statistics in Drinking Frequency

Section 6: Interesting of predicting data in other college

Section 1: General Look Of the Dataset

In here, I convey the dataset from JMP into excel, and use the code to call the excel dataset into pandas

import pandas as pd 
import altair as alt 
import pandas as pd 
!pip install openpyxl
df=pd.read_excel("Stastic Data for Project.xlsx",na_values="nan")
df

Collecting openpyxl
  Downloading openpyxl-3.0.10-py2.py3-none-any.whl (242 kB)
     |████████████████████████████████| 242 kB 9.4 MB/s 
?25hCollecting et-xmlfile
  Downloading et_xmlfile-1.1.0-py3-none-any.whl (4.7 kB)
Installing collected packages: et-xmlfile, openpyxl
Successfully installed et-xmlfile-1.1.0 openpyxl-3.0.10
WARNING: You are using pip version 20.1.1; however, version 22.1.2 is available.
You should consider upgrading via the '/root/venv/bin/python -m pip install --upgrade pip' command.
Do you have a clear understanding of what is alcoholic drinking? Have you experienced alcoholic drinking? Please select all the factors that applied to your reasons for alcolchol drinking. (if the you can not find your reason below, please fill out the blank in Other) If you responded "Other" to the previous question, put your answer here. Otherwise, type NA. What is your usual drinking level? What's your drinking frequency (per week)? What gender do you most identify as? How old will you be at December 31, 2022 (After your birthday this year)? What is your current year at UCI? GPA Mood
0 Confident No NaN NaN NaN Never Female 19.0 First year 3.28 NaN
1 Confident Yes Addiction to Acholoc NaN Moderate (tiny dizzy) 1-2 times Male 23.0 Second year 3.10 NaN
2 Very confident Yes Release stress from school works,Socailizing w... NaN Mild Never Female 20.0 Second year 3.40 NaN
3 Confident Yes Socailizing with peers NaN Mild 1-2 times Male 20.0 First year 3.68 NaN
4 Confident Yes Having fun na Mild 1-2 times Female 20.0 Fourth year 3.60 NaN
... ... ... ... ... ... ... ... ... ... ... ...
336 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN 6.0
337 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN 8.0
338 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN 1.0
339 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
340 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN 4.0

341 rows × 11 columns

We see that there are some of missing datas and bad datas cause by non-response bias and reponse bias. We might not 100 percent drop all the missing value since the datasample is small.

Also,in order to have a easier operation on the dataset, we need to “normalize” the dataframe. We want the column name to be shorter (since the column name is correspond to each survey questions)

df.rename({"Do you have a clear understanding of what is alcoholic drinking?":"understanding"},axis=1,inplace=True)
df.rename({"Have you experienced alcoholic drinking?":"experience"},axis=1,inplace=True)
df.rename({"Please select all the factors that applied to your reasons for alcolchol drinking. (if the you can not find your reason below, please fill out the blank in Other)":"reason"},axis=1,inplace=True)
df.rename({"If you responded 'Other' to the previous question, put your answer here. Otherwise, type NA.":"Otherreason"},axis=1,inplace=True)
df.rename({"What is your usual drinking level?":"level"},axis=1,inplace=True)
df.rename({"What's your drinking frequency (per week)?":"Freq"},axis=1,inplace=True)
df.rename({"What gender do you most identify as?":"gender"},axis=1,inplace=True)
df.rename({"How old will you be at December 31, 2022 (After your birthday this year)?":"Year"},axis=1,inplace=True)
df.rename({"What is your current year at UCI?":"grade"},axis=1,inplace=True)

However, I want to drop some of the nan values. Seeing columns “Other”, which contians much of nan values (since the much participants does not have other reason for drinking alcohol). Before I drop the actually nan values, I need drop this columns first.

df.drop('If you responded "Other" to the previous question, put your answer here. Otherwise, type NA.',axis=1,inplace=True)

df=df.dropna()

Section 2: Drinking Level

In here, I want to see the relation between Drinking level and student’s grade. Before that, I need unit the participants’ answers into same grading way. For example, there are answer for first year, meanwhile, there are answer for sophomore. So I would likely to change all sophomore grade into first year grade.

df["grade"].value_counts()

First year             82
Freshman               54
Second year            48
Sophomore              28
Third year             18
Fourth year            10
Junior                  7
Fifth year or later     2
Graduate Student        1
Senior                  1
Name: grade, dtype: int64

for i in df["grade"]:
    if i=="Freshman":
        df["grade"].replace({i:"First year"},inplace=True)
    if i=="Sophomore":
        df["grade"].replace({i:"Second year"},inplace=True)
    if i=="Junior":
        df["grade"].replace({i:"Third year"},inplace=True)
    if i=="Senior":
        df["grade"].replace({i:"Third year"},inplace=True)

/shared-libs/python3.7/py/lib/python3.7/site-packages/pandas/core/series.py:4515: SettingWithCopyWarning: 
A value is trying to be set on a copy of a slice from a DataFrame

See the caveats in the documentation: https://pandas.pydata.org/pandas-docs/stable/user_guide/indexing.html#returning-a-view-versus-a-copy
  method=method,

I set df2 as copy of df, so that I could operate more pandas operation without change the orginal dataframe.

df2=df.copy()

I would to see the numbers counts of each drinking level, so I set columns “Moderate”,”Mild”,and “Over drinking” to present the number of each cases.


df2["Moderate"]=0
df2["Mild"]=0
df2["Over drinking"]=0

df2.loc[df["level"]=="Moderate (tiny dizzy)","Moderate"]=1
df2.loc[df["level"]=="Mild","Mild"]=1
df2.loc[df["level"]=="Over drinking (e.g. Losing consciousness）","Over drinking"]=1

In here, I want to see how does the drinking level relate with grade. I want to show and compare the mean (which is the proportion of each grade on each cases) of level, because by grade distribution in the survey is not likely to be equal. Comparing proportion would be more meaningful than sum of cases. By having the visualize method, I also set up the color =counts to show first year and second year students are majority groups in my data, since they have deeper color as they have more counts.

cols=["Mild","Moderate","Over drinking"]
chart_list=[]
for i in cols:
    c=alt.Chart(df2).mark_bar().encode(
        x="grade",
        y=f"mean({i})",
        color="count()"
    )
    chart_list.append(c)
alt.hconcat(*chart_list)

I also want to see whether there is confounding variables (variables other than we concerns).Hence I present bar graph of gender and level. (In other words, I concern about gender might affect we draw out the conclusion). In the graph, below, we find out there are more female students in each cases, but it just implied more female students sample in my data.

chart_list2=[]
for i in cols:
    c=alt.Chart(df2).mark_bar().encode(
        x="gender",
        y=f"sum({i})",
        color="count()"
    )
    chart_list2.append(c)
alt.hconcat(*chart_list2)

df2
understanding experience reason level Freq gender Year grade GPA Mood Moderate Mild Over drinking
27 Very confident Yes Release stress from school works,Socailizing w... Mild Never Female 19.0 First year 2.500 7.0 0 1 0
28 Confident No Other Mild Never Female 20.0 Second year 3.400 5.0 0 1 0
29 Confident No Release stress from school works,Release emoti... Mild Never Female 20.0 Second year 3.600 6.0 0 1 0
30 Confident No Release emotion from relationship Moderate (tiny dizzy) 1-2 times Male 21.0 Second year 3.000 5.0 1 0 0
31 Very confident Yes Socailizing with peers,Having fun Mild 1-2 times Female 20.0 Second year 3.339 10.0 0 1 0
... ... ... ... ... ... ... ... ... ... ... ... ... ...
307 Very confident Yes Socailizing with peers,Having fun Moderate (tiny dizzy) 1-2 times Female 19.0 First year 3.914 5.0 1 0 0
308 Confident No Other Mild Never Female 20.0 Second year 3.694 1.0 0 1 0
309 Very confident Yes Release stress from school works,Socailizing w... Moderate (tiny dizzy) Never Female 20.0 Second year 3.800 10.0 1 0 0
311 Very confident Yes Socailizing with peers,Having fun Moderate (tiny dizzy) 1-2 times Male 21.0 First year 3.000 8.0 1 0 0
313 Very confident No Other Mild 3-4 times Female 19.0 First year 3.400 5.0 0 1 0

251 rows × 13 columns

After, I see the graphs, I am interesting using grade and gender to predict one’s drinking level. In here, I start to setting up the numercial counts for each variables. This help me to prepare to use the machine learning of logistic regression.

for i in df2["gender"].unique():
    df2[i]=0
    df2.loc[df2["gender"]==i,i]=1

for i in df2["grade"].unique():
    df2[i]=0
    df2.loc[df2["grade"]==i,i]=1
 
genderandgrade=[i for i in df2["gender"].unique()]+[i for i in df2["grade"].unique()]

I also split up train and test groups to see if fitting model accurate on the test groups or not. Seeing the result of clf.score of 0.5298, I suppose it does not have a very accurate prediction on the test group.

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
x_train,x_test,y_train,y_test=train_test_split(df2[genderandgrade],df2["level"],train_size=0.4)
clf=LogisticRegression()
clf.fit(x_train,y_train)
clf.score(x_test,y_test)

0.5695364238410596

I set up a Dataframe to contian all of my features. I put “Male” columns and “Second year” columns as 1, other as 0 , indicating I am a second grade male students. The following out is my drinking level, which is surprise me because to meet my drinking level


## Provide a example of me to try on 
JingxiFeng=pd.DataFrame({"Male":[1],"Female":[0],"Prefer not to say":[0],"Non-binary/Non-conforming":[0],"Genderqueer":[0],"Second year":[0],"First year":[1],"Fourth year":[0],"Fifth year or later":[0],"Third year":[0],"Graduate Student":[0]})
a=clf.predict(JingxiFeng[genderandgrade])
print(a)

['Mild']

Section 3: Descriptive Statistics in Drinking level

Having seeing both graphs and machine learning, I am interesting in setting up a hypothesis such that grade is association with drinking level. Hence, I am importing chi square table in order to check the association between Moderate drinking and grade.

import numpy as np
from scipy.stats import chi2_contingency
import seaborn as sns 
import matplotlib.pyplot as plt

The belowing is the DataFrame version of the chi-square table.

Chi_square_table= pd.crosstab(df2['grade'], df2['Moderate']) 
Chi_square_table.drop(index=["Fifth year or later","Graduate Student"],inplace=True)
Chi_square_table.rename({0:"Not Moderate",1:"Is Moderate"},axis=1)
Moderate Not Moderate Is Moderate
grade
First year 85 51
Fourth year 5 5
Second year 41 35
Third year 15 11

The below is the visual version of the Chi-square table. Seeing the data, I would have general guess that grade does not have strong association with Moderate level of drinking, because each data in the blank are close to the expect value (value that close to distribution if there is no relationship)

plt.figure(figsize=(15,8)) 
sns.heatmap(Chi_square_table, annot=True, cmap="YlGnBu")

<AxesSubplot:xlabel='Moderate', ylabel='grade'>
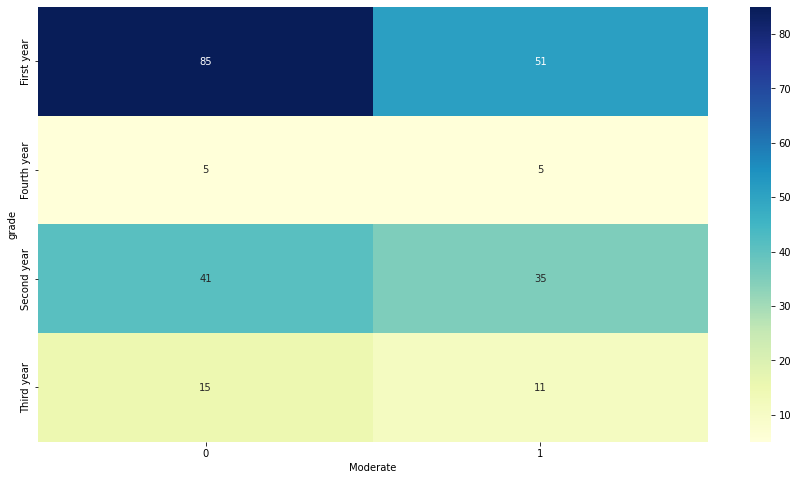
../../_images/JingxiFeng_35_1.png

The below are the test-stastistic and p-value. I have set up a significant level of 0.05, and seeing that the p-value far above this significant level, I conclude that there is no sufficant evidence show Grade is strongly associate with drinking level in this stastic Class samples.

test_statistic, pvalue, dof, expected = chi2_contingency(Chi_square_table)
test_statistic=test_statistic.round(3)
pvalue=pvalue.round(3)
f"the test stastistic is {test_statistic}, and the P-value is {pvalue} which is higher than the significant level of 0.05"

'the test stastistic is 1.841, and the P-value is 0.606 which is higher than the significant level of 0.05'

Section 4: Drinking Frequence

In this section, I am interesting of seeing the Drinking reason. I, first, rename all the data in the drinking frequence columns, and create columns for each individual frequence variable in order to get the counts for each one.

for i in df2.Freq.unique():
    df2[i]=0
    df2.loc[df2["Freq"]==i,i]=1

df2.rename({"Never":"Zerotime","1-2 times":"1to2","3-4 times":"3to4","More than 4 times":"4more"},axis=1,inplace=True)

In the interest of seeing visualize version of the how drinking frequence related with GPA, I set each drinkning group with interactive funciton on altair, so I could click on each other explictly. I also set up the tooltip equal GPA mean in order to see more clearly of each case’s GPA. We could notice that there drinking more than 4 time per week tend have higher GPA.(I am surpise the sample in my stastic class provide me this answer)

multi = alt.selection_multi()
alt.Chart(df2).mark_bar().encode(
    x="Freq",
    y=alt.Y("mean(GPA)",scale=alt.Scale(domain=(3,4))),
    color=alt.condition(multi, 'Freq', alt.value('lightgray')),
    tooltip=["mean(GPA)"]
).add_selection(multi)

Seeing the previous graph, I decide to see the value counts of whether “socilizing with peers” is in the reason of drinking.

for i in df2.index:
    if "Socailizing with peers" in df2["reason"].loc[i]:
        df2["reason"].loc[i]="social"
    elif "Socailizing with peers" not in df2["reason"].loc[i]:
        df2["reason"].loc[i]="no social"


    

/shared-libs/python3.7/py/lib/python3.7/site-packages/pandas/core/indexing.py:1637: SettingWithCopyWarning: 
A value is trying to be set on a copy of a slice from a DataFrame

See the caveats in the documentation: https://pandas.pydata.org/pandas-docs/stable/user_guide/indexing.html#returning-a-view-versus-a-copy
  self._setitem_single_block(indexer, value, name)

I, then, create a chart_list to see how social and no social reason relative with the drinking frequence.

cols1=["Zerotime","1to2","3to4","4more"]
chart_list3=[]

for i in cols1:
    single = alt.selection_single()
    c=alt.Chart(df2).mark_bar().encode(
        x="reason",
        y=f"mean({i})",
        color=alt.condition(single, 'reason', alt.value('lightgray')),
        tooltip="reason"
    ).add_selection(single)
    chart_list3.append(c)
alt.hconcat(*chart_list3)

In the interesting of seeing the relationship between GPA and drinking, I have also create the boxplot to compare groups of social drinking and no social drinking.

we see that,no social drinking group would have higher median GPA, but social group would have a higher maximum.

alt.Chart(df2).mark_boxplot().encode(
    x=alt.X("GPA",scale=alt.Scale(zero=False)),
    y="reason",
)

Next step, I am planing to use machine learning to find out the major influencer in drinking frequency. I set up the max_depth =3 and max_leaf_nodes equal 4 (there are 4 cases for drinking level) because I do not want the Classifier go too deep and too complex (as result of over fitting)

from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import log_loss
clf1=DecisionTreeClassifier(max_depth=3,max_leaf_nodes=4)
drinkingreason=["GPA","Mood"]+cols1

from sklearn import tree

Suprisingly, this model, base on the graph, show that the machine decide the class mostly base on the gender instead of grade. This is reasonable, because in my stastic class, no much variability in grade (since everyone is in grade one and two).

clf1.fit(df2[drinkingreason],df2["Freq"])
plt.figure(figsize=(10,10))
tree.plot_tree(
    clf1,
    feature_names=clf.feature_names_in_,
    class_names=clf1.classes_,
    filled=True
);
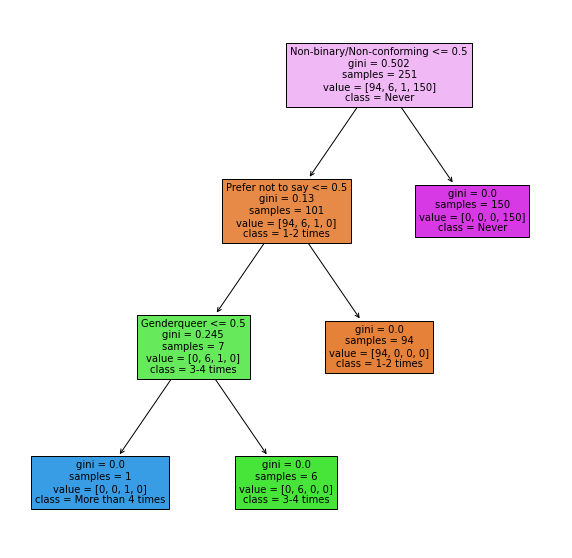
../../_images/JingxiFeng_53_0.png

Section 5: inferential statistics in Drinking Frequency

After seeing the above graphs and machine learning, I decide to conduct a one proportion z test and create a confident interval test.

!pip install statsmodels==0.13.2
from statsmodels.stats.proportion import proportions_ztest

Collecting statsmodels==0.13.2
  Downloading statsmodels-0.13.2-cp37-cp37m-manylinux_2_17_x86_64.manylinux2014_x86_64.whl (9.8 MB)
     |████████████████████████████████| 9.8 MB 20.7 MB/s 
?25hRequirement already satisfied: pandas>=0.25 in /shared-libs/python3.7/py/lib/python3.7/site-packages (from statsmodels==0.13.2) (1.2.5)
Requirement already satisfied: packaging>=21.3 in /shared-libs/python3.7/py/lib/python3.7/site-packages (from statsmodels==0.13.2) (21.3)
Requirement already satisfied: scipy>=1.3 in /shared-libs/python3.7/py/lib/python3.7/site-packages (from statsmodels==0.13.2) (1.7.3)
Requirement already satisfied: numpy>=1.17 in /shared-libs/python3.7/py/lib/python3.7/site-packages (from statsmodels==0.13.2) (1.21.6)
Collecting patsy>=0.5.2
  Downloading patsy-0.5.2-py2.py3-none-any.whl (233 kB)
     |████████████████████████████████| 233 kB 42.3 MB/s 
?25hRequirement already satisfied: python-dateutil>=2.7.3 in /shared-libs/python3.7/py-core/lib/python3.7/site-packages (from pandas>=0.25->statsmodels==0.13.2) (2.8.2)
Requirement already satisfied: pytz>=2017.3 in /shared-libs/python3.7/py/lib/python3.7/site-packages (from pandas>=0.25->statsmodels==0.13.2) (2022.1)
Requirement already satisfied: pyparsing!=3.0.5,>=2.0.2 in /shared-libs/python3.7/py/lib/python3.7/site-packages (from packaging>=21.3->statsmodels==0.13.2) (3.0.9)
Requirement already satisfied: six in /shared-libs/python3.7/py-core/lib/python3.7/site-packages (from patsy>=0.5.2->statsmodels==0.13.2) (1.16.0)
Installing collected packages: patsy, statsmodels
Successfully installed patsy-0.5.2 statsmodels-0.13.2
WARNING: You are using pip version 20.1.1; however, version 22.1.2 is available.
You should consider upgrading via the '/root/venv/bin/python -m pip install --upgrade pip' command.

In this test, I would to explore what the proportion of zero time drinking peer week in all UCI students I set up the number of success equal to case of 1 to 2 time and trials of all sample, and the hypothesize value in 0.37 (the null hypothesis). This mean I assume the proportion of all UCI students who drinking 1 to 2 time would not be approximate 37 percent (Alternative hypothesis).

##this show there are approximately 37 percent of stastic 7 class students drink 1 to 2 time peer weeks.
##which I want to reject this value of propotion in population.
null_value=(df2["1to2"].sum()/len(df2["1to2"])).round(3)
print(null_value)

0.375

number_of_successes=df2["1to2"].sum()
number_of_trials=len(df2["1to2"])
hypothesized_proportion=null_value
z_test_statistic,pvalue=proportions_ztest(count=number_of_successes,nobs=number_of_trials,value=hypothesized_proportion)

In here, I have set up a significant level of 0.05

z_test_statistic=z_test_statistic.round(3) 
pvalue=pvalue.round(5)
print(f"the statistic for the proportion ztest is {z_test_statistic},and the P-value is {pvalue}")
if pvalue>=0.05:
    print("the pvalue is equal and greater than 0.05 significant level,and hence fail to reject null hypothesis")
    print("Hence it shows there would likely to have 37 percent of UCI student drink 1 to 2 time per weeks")
elif pvalue<0.05:
    print("the pvalue is lower than 0.05 significant level,and hence reject null hypothesis")
    print("Hence it shows there would not likely to have 37 percent of UCI student drink 1 to 2 time per weeks")

the statistic for the proportion ztest is -0.016,and the P-value is 0.98699
the pvalue is equal and greater than 0.05 significant level,and hence fail to reject null hypothesis
Hence it shows there would likely to have 37 percent of UCI student drink 1 to 2 time per weeks

I also set a 95 precent confident interval fot the test in order to guess the true value within which interval in population (all UCI students)

from statsmodels.stats.proportion import proportion_confint
lower,upper=proportion_confint(count=number_of_successes,nobs=number_of_trials,alpha=(1-0.95))
lower=lower.round(3)
upper=upper.round(3)

print(f"we are 95% confident that the proportion for all UCI students who drink 1 to 2 times per weeks would between {lower} and {upper}")

we are 95% confident that the proportion for all UCI students who drink 1 to 2 times per weeks would between 0.315 and 0.434

Section 6: Interesting of predicting data in other college

In this cases, I want to use GPA and Gender as input to predict what is the drinking level and frequency be like in Duke Univeristy

Duke=pd.read_csv("gpa.csv",na_values=" ")
Duke.dropna()
gpa studyweek sleepnight out gender
0 3.890 50 6.0 3.0 female
1 3.900 15 6.0 1.0 female
2 3.750 15 7.0 1.0 female
3 3.600 10 6.0 4.0 male
4 4.000 25 7.0 3.0 female
5 3.150 20 7.0 3.0 male
6 3.250 15 6.0 1.0 female
7 3.925 10 8.0 3.0 female
8 3.428 12 8.0 2.0 female
9 3.800 2 8.0 4.0 male
10 3.900 10 8.0 1.0 female
11 2.900 30 6.0 2.0 female
12 3.925 30 7.0 2.0 female
13 3.650 21 9.0 3.0 female
14 3.750 10 8.5 3.5 female
15 4.670 14 6.5 3.0 male
16 3.100 12 7.5 3.5 male
17 3.800 12 8.0 1.0 female
18 3.400 4 9.0 3.0 female
19 3.575 45 6.5 1.5 female
20 3.850 6 7.0 2.5 female
21 3.400 10 7.0 3.0 female
22 3.500 12 8.0 2.0 male
23 3.600 13 6.0 3.5 female
24 3.825 35 8.0 4.0 female
25 3.925 10 8.0 3.0 female
26 4.000 40 8.0 3.0 female
27 3.425 14 9.0 3.0 female
28 3.750 30 6.0 0.0 female
29 3.150 8 6.0 0.0 female
30 3.400 8 6.5 2.0 female
31 3.700 20 7.0 1.0 female
32 3.360 40 7.0 1.0 female
33 3.700 15 7.0 1.5 male
34 3.700 25 5.0 1.0 female
35 3.600 10 7.0 2.0 female
36 3.825 18 7.0 1.5 female
37 3.200 15 6.0 1.0 female
38 3.500 30 8.0 3.0 male
39 3.500 11 7.0 1.5 female
40 3.000 28 6.0 1.5 female
41 3.980 4 7.0 1.5 female
42 3.700 4 5.0 1.0 male
43 3.810 25 7.5 2.5 female
44 4.000 42 5.0 1.0 female
45 3.100 3 7.0 2.0 male
46 3.400 42 9.0 2.0 male
47 3.500 25 8.0 2.0 male
48 3.650 20 6.0 2.0 female
49 3.700 7 8.0 2.0 female
50 3.100 6 8.0 1.0 female
51 4.000 20 7.0 3.0 female
52 3.350 45 6.0 2.0 female
53 3.541 30 7.5 1.5 female
54 2.900 20 6.0 3.0 female 

for i in Duke.gender.unique():
    Duke[i]=0
    Duke.loc[Duke["gender"]==i,i]=1

Duke.rename({"gpa":"GPA","female":"Female","male":"Male"},axis=1,inplace=True)

In the following code, I find out that all 55 sample in the Duke Univeristy data does not drink at all per weeks. (notice that, it might cause by the parameter of GAP, which means, Duke’s students tend to have higher GPA, and so lead to more likely to have the output of never drink per week). Another major reason for casuing this because there are still some response bias data in orignal dataset, which might cause the wrong input.

clf_freq=LogisticRegression()
clf.fit(df2[["Female","Male","GPA"]],df2["Freq"])
Duke["Freq"]=clf.predict(Duke[["Female","Male","GPA"]])
print(Duke["Freq"].value_counts())

Never    55
Name: Freq, dtype: int64


clf_level=LogisticRegression()
clf.fit(df2[["Female","Male","GPA"]],df2["level"])
Duke["level"]=clf.predict(Duke[["Female","Male","GPA"]])
print(Duke["level"].value_counts())

Mild                     51
Moderate (tiny dizzy)     4
Name: level, dtype: int64

In here, since there is not comparsion between UCI and Duke drinking frequency, I decide to find out the comparision of drinking level.

for i in Duke.index:
    if Duke["level"].loc[i]=="Moderate (tiny dizzy)":
        Duke["level"].loc[i]="Moderate"

/shared-libs/python3.7/py/lib/python3.7/site-packages/pandas/core/indexing.py:1637: SettingWithCopyWarning: 
A value is trying to be set on a copy of a slice from a DataFrame

See the caveats in the documentation: https://pandas.pydata.org/pandas-docs/stable/user_guide/indexing.html#returning-a-view-versus-a-copy
  self._setitem_single_block(indexer, value, name)

In conclusion, we predict that Duke University might have less Moderate drinking students and higher Mild drinking students in UCI.


for i in Duke["level"].unique():
    a=(Duke["level"]==i).sum()/len(Duke["level"])-(df2[i].sum()/len(df2[i]))
    a=(a*100).round(2)
    if a>0:
        print(f"Duke University has {a} percent higher of {i} level of drinking student than UCI")
    elif a<0:
        print(f"Duke University has {a} percent lower of {i} level drinking student than UCI")
    elif a==0:
        print(f"Duke University has the same percent of {i} level drinking student as UCI")




Duke University has 37.35 percent higher of Mild level of drinking student than UCI
Duke University has -34.56 percent lower of Moderate level drinking student than UCI

Summary

Over, I ultize the alt chart and machine learning find out that, base on my survey dataset, UCI students might likely to have moderate level of drinking. They would likely to have 1 to 2 times per weeks due to more activities of socialing with peers. In general, the chi-square test tell me that there are less there are no much strong association between grade and drinking level in UCI stastic 7 class students. Meanwhile, both one proportion z-test and confident level tell me that there would likely to have 37 percent of UCI students drink 1 to 2 time per weeks. Last, by using machine learning to compare Duke Univeristy and UCI, it predict that Duke University might tend to have less drinking frequency, but higher Mild level of drinking.

Either summarize what you did, or summarize the results. Maybe 3 sentences.

References

The main dataset (Stastic Data of Project) is created by my own.

https://altair-viz.github.io/altair-tutorial/notebooks/04-Compound-charts.html (interactive in altair: This website provide all guideline for me to see different interactive funciton in altair. I check them by seeing the menu on the webiste)

https://www.statology.org/one-proportion-z-test-python/ (one proportion z-test: This website teach me how to create one proportion z-test by showing me coding and relative pandas knolwedge behind it)

https://akshay-a.medium.com/confidence-interval-for-population-proportion-basic-understanding-in-python-56b8cc5f8320 (confident level: This website show me how to create a confident level test with relative confident interval. The code it provide inspire me to create my own 95 percent confident level interval test)

  • List other references that you found helpful.

Created in deepnote.com Created in Deepnote

previous

Exoplanet Candidate Analysis

next

Real vs fake faces

By Christopher Davis
© Copyright 2022.