Week 5 Videos
Contents
Week 5 Videos¶
Unpacking¶
Warm-up task: Define
ncolto be the number of columns in the Spotify dataset.
import pandas as pd
df = pd.read_csv("../data/spotify_dataset.csv", na_values=" ").dropna()
t = df.shape
t[1]
23
_, ncol = df.shape
ncol
23
_
1545
import matplotlib.pyplot as plt
t = plt.subplots()

type(t)
tuple
type(t[0])
matplotlib.figure.Figure
type(t[1])
matplotlib.axes._subplots.AxesSubplot
# tuple unpacking
fig, ax = plt.subplots()

type(fig)
matplotlib.figure.Figure
type(ax)
matplotlib.axes._subplots.AxesSubplot
for a,b in df.groupby("Artist"):
print(a)
display(b)
break
*NSYNC
| Index | Highest Charting Position | Number of Times Charted | Week of Highest Charting | Song Name | Streams | Artist | Artist Followers | Song ID | Genre | ... | Danceability | Energy | Loudness | Speechiness | Acousticness | Liveness | Tempo | Duration (ms) | Valence | Chord | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 690 | 691 | 184 | 1 | 2020-12-18--2020-12-25 | Merry Christmas, Happy Holidays | 6,635,128 | *NSYNC | 1564750.0 | 4v9WbaxW8HdjqfUiWYWsII | ['boy band', 'dance pop', 'pop', 'post-teen pop'] | ... | 0.643 | 0.939 | -3.967 | 0.0463 | 0.104 | 0.881 | 104.999 | 255307.0 | 0.756 | F |
1 rows × 23 columns
Generating data for linear regression¶
from sklearn.datasets import make_regression
help(make_regression)
Help on function make_regression in module sklearn.datasets._samples_generator:
make_regression(n_samples=100, n_features=100, *, n_informative=10, n_targets=1, bias=0.0, effective_rank=None, tail_strength=0.5, noise=0.0, shuffle=True, coef=False, random_state=None)
Generate a random regression problem.
The input set can either be well conditioned (by default) or have a low
rank-fat tail singular profile. See :func:`make_low_rank_matrix` for
more details.
The output is generated by applying a (potentially biased) random linear
regression model with `n_informative` nonzero regressors to the previously
generated input and some gaussian centered noise with some adjustable
scale.
Read more in the :ref:`User Guide <sample_generators>`.
Parameters
----------
n_samples : int, default=100
The number of samples.
n_features : int, default=100
The number of features.
n_informative : int, default=10
The number of informative features, i.e., the number of features used
to build the linear model used to generate the output.
n_targets : int, default=1
The number of regression targets, i.e., the dimension of the y output
vector associated with a sample. By default, the output is a scalar.
bias : float, default=0.0
The bias term in the underlying linear model.
effective_rank : int, default=None
if not None:
The approximate number of singular vectors required to explain most
of the input data by linear combinations. Using this kind of
singular spectrum in the input allows the generator to reproduce
the correlations often observed in practice.
if None:
The input set is well conditioned, centered and gaussian with
unit variance.
tail_strength : float, default=0.5
The relative importance of the fat noisy tail of the singular values
profile if `effective_rank` is not None. When a float, it should be
between 0 and 1.
noise : float, default=0.0
The standard deviation of the gaussian noise applied to the output.
shuffle : bool, default=True
Shuffle the samples and the features.
coef : bool, default=False
If True, the coefficients of the underlying linear model are returned.
random_state : int, RandomState instance or None, default=None
Determines random number generation for dataset creation. Pass an int
for reproducible output across multiple function calls.
See :term:`Glossary <random_state>`.
Returns
-------
X : ndarray of shape (n_samples, n_features)
The input samples.
y : ndarray of shape (n_samples,) or (n_samples, n_targets)
The output values.
coef : ndarray of shape (n_features,) or (n_features, n_targets)
The coefficient of the underlying linear model. It is returned only if
coef is True.
t = make_regression(n_features=1)
type(t)
tuple
len(t)
2
type(t[0])
numpy.ndarray
t[0].shape
(100, 1)
type(t[1])
numpy.ndarray
t[1].shape
(100,)
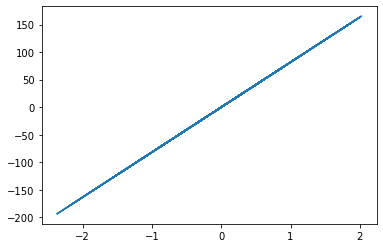
fig, ax = plt.subplots()
ax.plot(t[0], t[1])
[<matplotlib.lines.Line2D at 0x7f8e59a4eb10>]
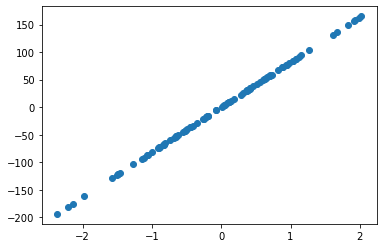
fig, ax = plt.subplots()
ax.scatter(t[0], t[1])
<matplotlib.collections.PathCollection at 0x7f8e59a8d610>
X,y = make_regression(n_samples = 10, n_features=1, coef=True)
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
/var/folders/8j/gshrlmtn7dg4qtztj4d4t_w40000gn/T/ipykernel_90918/737216033.py in <module>
----> 1 X,y = make_regression(n_samples = 10, n_features=1, coef=True)
ValueError: too many values to unpack (expected 2)
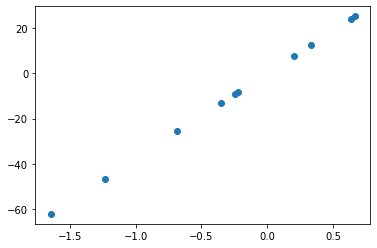
X,y,m = make_regression(n_samples = 10, n_features=1, coef=True)
m
array(37.61300837)
fig, ax = plt.subplots()
ax.scatter(X,y)
<matplotlib.collections.PathCollection at 0x7f8e59a8d590>
Linear regression using scikit-learn¶
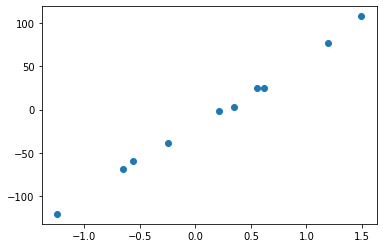
X,y,m = make_regression(n_samples = 10, n_features=1, coef=True, noise=5, bias=-17.4)
fig, ax = plt.subplots()
ax.scatter(X,y)
<matplotlib.collections.PathCollection at 0x7f8e4b0f75d0>
from sklearn.linear_model import LinearRegression
reg = LinearRegression()
type(reg)
sklearn.linear_model._base.LinearRegression
reg.fit(X,y)
LinearRegression()
reg.coef_
array([80.74305618])
m
array(80.45838668)
reg.intercept_
-18.956015204674802
pred = reg.predict(X)
pred
array([ -64.36020915, -71.53057174, 77.7462882 , -38.87491328,
9.15078824, -1.67347246, 101.57870959, 26.11546954,
-119.41690634, 30.87178162])
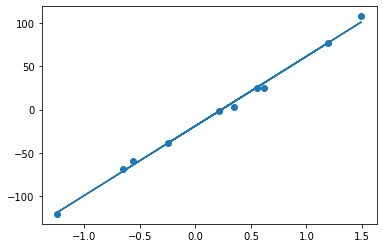
fig, ax = plt.subplots()
ax.scatter(X,y)
ax.plot(X,pred)
[<matplotlib.lines.Line2D at 0x7f8e4b37aa50>]
Linear regression with a real dataset¶
Find the line of best fit for “Acousticness” vs “Energy” from the Spotify dataset.
df = pd.read_csv("../data/spotify_dataset.csv", na_values=" ").dropna()
import altair as alt
alt.Chart(df).mark_circle().encode(
x="Acousticness",
y="Energy"
)
reg = LinearRegression()
reg.fit(df["Acousticness"],df["Energy"])
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
/var/folders/8j/gshrlmtn7dg4qtztj4d4t_w40000gn/T/ipykernel_90918/2831094536.py in <module>
----> 1 reg.fit(df["Acousticness"],df["Energy"])
~/miniconda3/envs/math10s22/lib/python3.7/site-packages/sklearn/linear_model/_base.py in fit(self, X, y, sample_weight)
661
662 X, y = self._validate_data(
--> 663 X, y, accept_sparse=accept_sparse, y_numeric=True, multi_output=True
664 )
665
~/miniconda3/envs/math10s22/lib/python3.7/site-packages/sklearn/base.py in _validate_data(self, X, y, reset, validate_separately, **check_params)
579 y = check_array(y, **check_y_params)
580 else:
--> 581 X, y = check_X_y(X, y, **check_params)
582 out = X, y
583
~/miniconda3/envs/math10s22/lib/python3.7/site-packages/sklearn/utils/validation.py in check_X_y(X, y, accept_sparse, accept_large_sparse, dtype, order, copy, force_all_finite, ensure_2d, allow_nd, multi_output, ensure_min_samples, ensure_min_features, y_numeric, estimator)
974 ensure_min_samples=ensure_min_samples,
975 ensure_min_features=ensure_min_features,
--> 976 estimator=estimator,
977 )
978
~/miniconda3/envs/math10s22/lib/python3.7/site-packages/sklearn/utils/validation.py in check_array(array, accept_sparse, accept_large_sparse, dtype, order, copy, force_all_finite, ensure_2d, allow_nd, ensure_min_samples, ensure_min_features, estimator)
771 "Reshape your data either using array.reshape(-1, 1) if "
772 "your data has a single feature or array.reshape(1, -1) "
--> 773 "if it contains a single sample.".format(array)
774 )
775
ValueError: Expected 2D array, got 1D array instead:
array=[0.127 0.0383 0.335 ... 0.184 0.249 0.433 ].
Reshape your data either using array.reshape(-1, 1) if your data has a single feature or array.reshape(1, -1) if it contains a single sample.
df["Acousticness"]
0 0.12700
1 0.03830
2 0.33500
3 0.04690
4 0.02030
...
1551 0.00261
1552 0.24000
1553 0.18400
1554 0.24900
1555 0.43300
Name: Acousticness, Length: 1545, dtype: float64
df[["Acousticness"]]
| Acousticness | |
|---|---|
| 0 | 0.12700 |
| 1 | 0.03830 |
| 2 | 0.33500 |
| 3 | 0.04690 |
| 4 | 0.02030 |
| ... | ... |
| 1551 | 0.00261 |
| 1552 | 0.24000 |
| 1553 | 0.18400 |
| 1554 | 0.24900 |
| 1555 | 0.43300 |
1545 rows × 1 columns
reg.fit(df[["Acousticness"]],df["Energy"])
LinearRegression()
reg.intercept_
0.7205632317364903
reg.coef_
array([-0.35010056])
Predict \(y = -0.35\cdot x + 0.72\).
