Real vs fake faces
Contents
Real vs fake faces¶
Author: Xiangbo Gao, xiangbog@uci.edu, https://github.com/XiangboGaoBarry
Course Project, UC Irvine, Math 10, S22
Introduction¶
This project use the dataset from https://www.kaggle.com/datasets/uditsharma72/real-vs-fake-faces, aiming to train a model to distinguish between fake and real images.
For adapting the 100MB disk limit of deepnote and for simplicity, I removed all the medium and hard fake images from the dataset. Around 60% of real images are also deleted, which results in 240 fake images and 343 real images.
By default, each image is reshaped to 32 by 32. I also evaluate the performance of different image size in the last section
Main portion of the project¶
Data preprocessing and visualization¶
from PIL import Image
import os
import torch
import pandas as pd
import numpy as np
import altair as alt
from tqdm import tqdm
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
import random
Data loading¶
Loading all the images to a dataframe or a python list.
The python list version is used for training neural networks
dim = 32
### Loading data ###
# return dataframe if to_df is True,
# otherwise return a list of unshuffled (image, label) pairs
def read_images(path="data", to_df=True, dim=32):
if to_df:
data_dict = {f"pixel{i}":[] for i in range(dim*dim*3)}
data_dict["label"] = []
df = pd.DataFrame(data_dict)
else:
img_list = []
idx = 0
for label, classname in enumerate(["fake", 'real']):
class_path = f"{path}/{classname}"
for filename in tqdm(os.listdir(class_path)):
image_path = f"{class_path}/{filename}"
try:
img = Image.open(image_path)
img = img.resize((32,32))
except Exception as e:
raise e
if to_df:
img_np = np.array(img)
img_label = np.concatenate((img_np.flatten(), np.array([label])))
df.loc[idx] = list(img_label)
idx += 1
else:
img_list.append((img, label))
return df if to_df else img_list
def split_set(dataset, ratio=0.8, is_df=True):
if is_df:
return train_test_split(dataset.iloc[:,:-1], dataset["label"], train_size=ratio)
else:
length = len(dataset)
dataset = random.sample(dataset, length)
return dataset[:int(ratio*length)], dataset[int((1-ratio)*length):]
df = read_images()
100%|██████████| 240/240 [00:06<00:00, 36.58it/s]
100%|██████████| 343/343 [00:09<00:00, 34.47it/s]
X_train, X_test, y_train, y_test = split_set(df, 0.8)
alt.Chart(df[["label"]], title="target distribution").mark_bar(size=10).encode(
x = "label:N",
y = "count()",
color = "label:N"
)
fake_img = df[df["label"]==0].iloc[1].to_numpy()[:-1].reshape(dim, dim, 3).astype(int)
real_img = df[df["label"]==1].iloc[1].to_numpy()[:-1].reshape(dim, dim, 3).astype(int)
print("fake image")
plt.imshow(fake_img)
plt.show()
print("real image")
plt.imshow(real_img)
plt.show()
fake image

real image

Logistic Regression with different regularization strength¶
from sklearn.linear_model import LogisticRegression
test_acc = []
weight_decays = [10,1,0.1,0.01,1e-3,1e-4,1e-5,1e-6,0]
for wd in tqdm(weight_decays):
pipe = Pipeline([
("scaler", StandardScaler()),
('reg', LogisticRegression(penalty='l2', C=wd, max_iter=5000) if wd
else LogisticRegression(max_iter=5000))
])
pipe.fit(X_train, y_train)
test_acc.append(pipe.score(X_test, y_test))
100%|██████████| 9/9 [00:07<00:00, 1.13it/s]
print(test_acc)
plt.plot(weight_decays, test_acc)
plt.ylabel("test accuracy log")
plt.xlabel("weight decays")
plt.xscale('log')
plt.show()
plt.plot(weight_decays, test_acc)
plt.ylabel("test accuracy")
plt.xlabel("weight decays")
plt.show()
[0.5641025641025641, 0.5641025641025641, 0.5555555555555556, 0.5555555555555556, 0.5726495726495726, 0.5811965811965812, 0.5811965811965812, 0.5811965811965812, 0.5641025641025641]
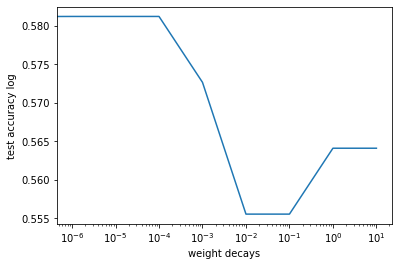
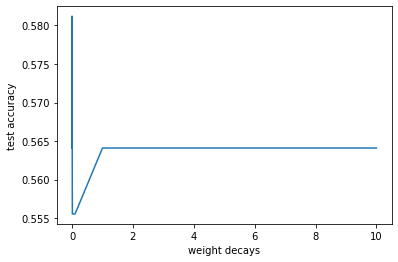
Analysis¶
The highest accuracy achieved using logistic regression is \(58.1\%\), where l2 penalty is set to be \(1e-6\)
As the coefficient of l2 penalty increase, the test accuracy tend to decrease. This is beacause the model experiences a very severe underfitting. Therefore, the model complexity needs to be increased.
Notice that the model with l2 penalty=0 also has low accuracy.
Polynomial Regression with different degrees¶
def polynomial(df, n):
cols = dim*dim*3
df = df.copy()
df_sub = df[:cols].copy()
for p in range(2,n+1):
df_ploy = df_sub**2
ploy_names = {oname: f"{oname}_poly{p}" for oname in df_sub.columns}
df_ploy = df_ploy.rename(columns=ploy_names)
df[list(ploy_names.values())] = df_ploy
return df
Because the data has very high dimension, instead of using sklearn.preprocessins.PloynomialFeatures
to calculate all 2nd degree combinations, we define ploy which only calculate x^2 for each dimension.
from sklearn.preprocessing import PolynomialFeatures
test_acc = []
ploy = [1,2,3,4,5,6]
for p in tqdm(ploy):
pipe = Pipeline([
("scaler", StandardScaler()),
('reg', LogisticRegression(penalty='l2', C=1e-6, max_iter=5000))
])
X_train_ploy = polynomial(X_train, p)
pipe.fit(X_train_ploy, y_train)
X_test_ploy = polynomial(X_test, p)
test_acc.append(pipe.score(X_test_ploy, y_test))
print(test_acc)
plt.plot(ploy, test_acc)
plt.ylabel("test accuracy")
plt.xlabel("polynomials")
plt.show()
[0.5811965811965812, 0.5811965811965812, 0.5811965811965812, 0.5811965811965812, 0.5811965811965812, 0.5811965811965812]

Unfortunately, simply increase the degree of each dimension does not help.
Decision Tree¶
Visualize the feature importance of the decision tree or random forest classifiers.
The feature importances are reshaped to the same shape of a image. For better visualization, A gaussian filter with \(\sigma = 5\) is applied to the reshaped feature importance.
The display results will be self-explaintory.
def show_attention(clf):
from scipy.ndimage import gaussian_filter
fig, ax = plt.subplots(1, 3, figsize=(10,8))
importances = clf.feature_importances_.reshape(dim,dim, 3).mean(-1)
filtered_importance = gaussian_filter(importances, sigma=5)
normalized_importance = filtered_importance/(filtered_importance.max()-filtered_importance.min())
ax[0].imshow(filtered_importance, cmap='gray')
ax[0].set_title("attention map")
ax[1].imshow(real_img/255.)
ax[1].set_title("face image")
ax[2].imshow(real_img/255. * 0.2 + np.expand_dims(normalized_importance,-1).repeat(3, axis=2) * 0.7)
ax[2].set_title("face image + attention map")
plt.show()
from sklearn.tree import DecisionTreeClassifier
leaf_nodes = range(20,300,30)
max_depths = range(2,20,2)
test_acc = np.zeros((len(leaf_nodes), len(max_depths)))
for idx_leaf, leaf_node in tqdm(enumerate(leaf_nodes)):
for idx_depth, max_depth in enumerate(max_depths):
tree = DecisionTreeClassifier(max_depth=max_depth, max_leaf_nodes=leaf_node)
tree.fit(X_train, y_train)
test_acc[idx_leaf, idx_depth] = tree.score(X_test, y_test)
10it [02:34, 15.47s/it]
fig, ax = plt.subplots(figsize=(10,10))
im = ax.imshow(test_acc)
ax.set_xticks(np.arange(len(max_depths)), labels=max_depths)
ax.set_yticks(np.arange(len(leaf_nodes)), labels=leaf_nodes)
for i in range(len(leaf_nodes)):
for j in range(len(max_depths)):
text = ax.text(j, i, round(test_acc[i, j],3),
ha="center", va="center", color="black")
ax.set_title("accuacy (Decision Tree)")
ax.set_xlabel("max depth")
ax.set_ylabel("max leaf nodes")
fig.tight_layout()
plt.show()
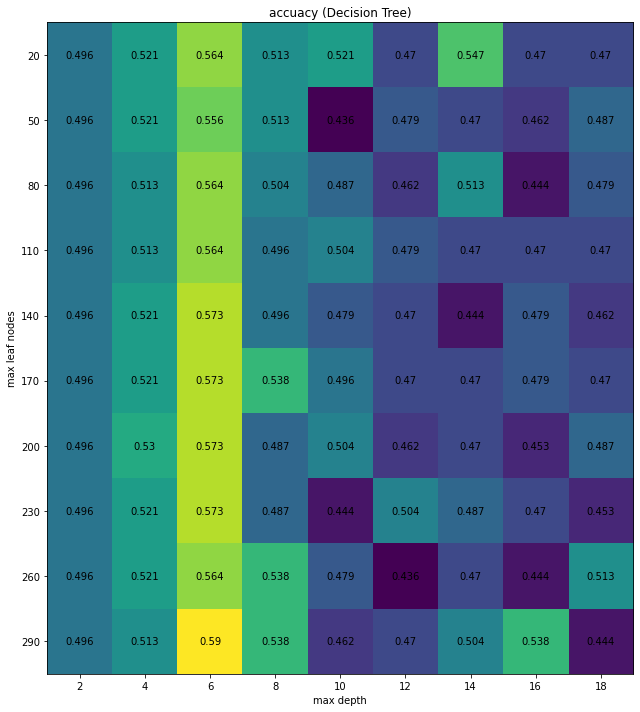
from sklearn.tree import DecisionTreeClassifier
tree = DecisionTreeClassifier(max_depth=6, max_leaf_nodes=290)
tree.fit(X_train, y_train)
test_acc = tree.score(X_test, y_test)
print(tree.score(X_train, y_train))
print(test_acc)
0.7424892703862661
0.5811965811965812
show_attention(tree)

Analysis¶
Decision tree reaches 58.11% accuracy in classification. Although it is not very high, it does tend to pay attention to the facial features of each face image
Random Forest¶
from sklearn.ensemble import RandomForestClassifier
leaf_nodes = range(20,300,30)
max_depths = range(2,20,2)
test_acc = np.zeros((len(leaf_nodes), len(max_depths)))
for idx_leaf, leaf_node in tqdm(enumerate(leaf_nodes)):
for idx_depth, max_depth in enumerate(max_depths):
tree = RandomForestClassifier(n_estimators=100, max_depth=max_depth, max_leaf_nodes=leaf_node)
tree.fit(X_train, y_train)
test_acc[idx_leaf, idx_depth] = tree.score(X_test, y_test)
10it [03:28, 20.88s/it]
fig, ax = plt.subplots(figsize=(10,10))
im = ax.imshow(test_acc)
ax.set_xticks(np.arange(len(max_depths)), labels=max_depths)
ax.set_yticks(np.arange(len(leaf_nodes)), labels=leaf_nodes)
for i in range(len(leaf_nodes)):
for j in range(len(max_depths)):
text = ax.text(j, i, round(test_acc[i, j],3),
ha="center", va="center", color="black")
ax.set_title("accuacy (random forest)")
ax.set_xlabel("max depth")
ax.set_ylabel("max leaf nodes")
fig.tight_layout()
plt.show()
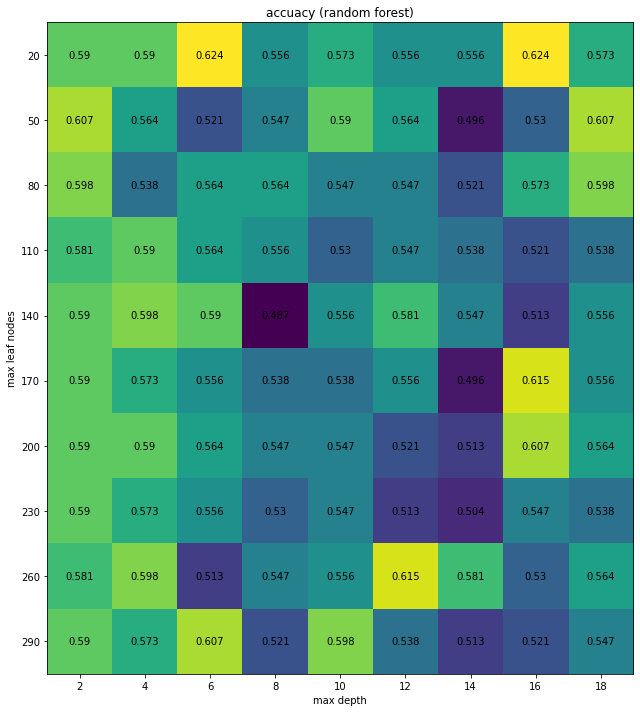
from sklearn.ensemble import RandomForestClassifier
forest = DecisionTreeClassifier(max_depth=16, max_leaf_nodes=20)
forest.fit(X_train, y_train)
test_acc = forest.score(X_test, y_test)
print(forest.score(X_train, y_train))
print(test_acc)
0.8669527896995708
0.5470085470085471
show_attention(forest)

Analysis¶
Random forest reaches 62.4% accuracy in classification. Similiar to decision tree, it tends to pay attention to the facial features of each face image
Fully Connected Neural Networks¶
Data loading and preprocessing
This block of code basically putting the list of images to a pytorch dataloader module. The data is loading in this way for the ease of changing some hyper-parameters, e.g. batch_size.
Reference: https://pytorch.org/tutorials/beginner/basics/data_tutorial.html
import torch
import torchvision
import torchvision.transforms as transforms
import torch.optim as optim
transform = transforms.Compose(
[transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])
dataset = read_images(to_df=False)
class Dataset:
def __init__(self, data, transform):
self.data = data
self.transform = transform
def __len__(self):
return len(self.data)
def __getitem__(self, idx):
img, label = self.data[idx]
if self.transform:
return self.transform(img), label
else:
return img, label
trainset, testset = split_set(dataset, is_df=False)
traindata = Dataset(trainset, transform=transform)
testdata = Dataset(testset, transform=transform)
batch_size = 20
trainloader = torch.utils.data.DataLoader(traindata, batch_size=batch_size,
shuffle=True)
test_loader = torch.utils.data.DataLoader(testdata, batch_size=batch_size,
shuffle=False)
100%|██████████| 240/240 [00:05<00:00, 47.77it/s]
100%|██████████| 343/343 [00:07<00:00, 48.93it/s]
Model trainning and evaluation
This block of code includes the full process of training and inference a basic neural networks, including criterion (loss function), model forwarding, backpropagation, accuracy calculating, etc.
Reference: https://pytorch.org/tutorials/beginner/blitz/cifar10_tutorial.html
def train_eval(net, conv=False):
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(net.parameters(), weight_decay=1e-3, lr=0.001)
train_loss = []
test_loss = []
test_acc = []
for epoch in range(100):
running_loss_train = 0.0
running_loss_test = 0.0
succ = 0
for i, data in enumerate(trainloader, 0):
inputs, labels = data
if not conv:
inputs = inputs.reshape(inputs.shape[0],-1)
optimizer.zero_grad()
outputs = net(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
running_loss_train += loss.item()
train_loss.append(running_loss_train / i)
with torch.no_grad():
for i, data in enumerate(test_loader, 0):
inputs, labels = data
if not conv:
inputs = inputs.reshape(inputs.shape[0],-1)
outputs = net(inputs)
loss = criterion(outputs, labels)
running_loss_test += loss.item()
succ += (torch.argmax(outputs, axis=1) == labels).int().sum()
test_loss.append(running_loss_test / i)
print(f"trainloss:{running_loss_train} | testloss:{running_loss_test} | accuarcy:{succ/len(testdata)}")
test_acc.append(succ/len(testdata))
return train_loss, test_loss, test_acc
Model definition
Define the architecture of model. A very basic fully connected neural networks including 4 linear layers and 3 activation layers.
Reference: https://pytorch.org/tutorials/beginner/blitz/cifar10_tutorial.html
import torch.nn as nn
import torch.nn.functional as F
class FCNet(nn.Module):
def __init__(self, dim=32):
super().__init__()
self.fc1 = nn.Linear(3*dim*dim, 300)
self.fc2 = nn.Linear(300, 100)
self.fc3 = nn.Linear(100, 30)
self.fc4 = nn.Linear(30, 2)
def forward(self, x):
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = F.relu(self.fc3(x))
x = self.fc4(x)
return x
fcnet = FCNet()
train_loss, test_loss, test_acc = train_eval(fcnet)
trainloss:16.56961476802826 | testloss:15.754675149917603 | accuarcy:0.5931477546691895
trainloss:15.426325619220734 | testloss:14.719747364521027 | accuarcy:0.6531049013137817
trainloss:14.581692814826965 | testloss:14.169351756572723 | accuarcy:0.6980727910995483
trainloss:13.379856526851654 | testloss:12.90772658586502 | accuarcy:0.7601712942123413
trainloss:11.982272148132324 | testloss:12.41127060353756 | accuarcy:0.7880085706710815
trainloss:10.84951938688755 | testloss:11.971969366073608 | accuarcy:0.7580299973487854
trainloss:8.479621469974518 | testloss:13.28071266412735 | accuarcy:0.7773019075393677
trainloss:8.746856726706028 | testloss:15.003946974873543 | accuarcy:0.7880085706710815
trainloss:7.791025534272194 | testloss:11.875941455364227 | accuarcy:0.8115631937980652
trainloss:5.54453968256712 | testloss:11.76796056702733 | accuarcy:0.8436830639839172
trainloss:5.161540012806654 | testloss:14.999820500612259 | accuarcy:0.8137044906616211
trainloss:5.725048944354057 | testloss:12.930241238325834 | accuarcy:0.7987151741981506
trainloss:3.747292583808303 | testloss:12.015180356800556 | accuarcy:0.8736616969108582
trainloss:2.1185702411457896 | testloss:12.951560331508517 | accuarcy:0.8758029937744141
trainloss:2.431673549115658 | testloss:13.219179203733802 | accuarcy:0.8715203404426575
trainloss:1.2626928817480803 | testloss:14.874831549823284 | accuarcy:0.8522483706474304
trainloss:1.7012146145571023 | testloss:14.514655915088952 | accuarcy:0.8800856471061707
trainloss:3.0909752533771098 | testloss:13.734901558607817 | accuarcy:0.8886509537696838
trainloss:1.2858465611934662 | testloss:13.45237692585215 | accuarcy:0.8865096569061279
trainloss:1.6616925185080618 | testloss:16.93788402946666 | accuarcy:0.8650963306427002
trainloss:2.885765337385237 | testloss:13.180429468862712 | accuarcy:0.8822270035743713
trainloss:4.004854544997215 | testloss:16.26563262194395 | accuarcy:0.8372591137886047
trainloss:2.8885456640273333 | testloss:14.048117505386472 | accuarcy:0.8693790435791016
trainloss:1.4832028076052666 | testloss:13.930955037940294 | accuarcy:0.8650963306427002
trainloss:0.7459619310684502 | testloss:14.550618639914319 | accuarcy:0.8779443502426147
trainloss:1.199125180253759 | testloss:16.474907412193716 | accuarcy:0.8586723804473877
trainloss:2.0266633764840662 | testloss:15.030181603971869 | accuarcy:0.8758029937744141
trainloss:0.8391441497951746 | testloss:15.58846954535693 | accuarcy:0.8800856471061707
trainloss:0.2501855493756011 | testloss:16.189931862987578 | accuarcy:0.8886509537696838
trainloss:0.12236911931540817 | testloss:17.09673395822756 | accuarcy:0.8822270035743713
trainloss:0.21307024272391573 | testloss:16.995193215785548 | accuarcy:0.8886509537696838
trainloss:0.08319775595737156 | testloss:16.667086978559382 | accuarcy:0.8865096569061279
trainloss:0.1053560926229693 | testloss:17.412625364551786 | accuarcy:0.8886509537696838
trainloss:0.07177511349436827 | testloss:17.16889216992422 | accuarcy:0.8822270035743713
trainloss:0.2600559491402237 | testloss:17.465176820842316 | accuarcy:0.8907923102378845
trainloss:0.12636436757748015 | testloss:18.085312008101027 | accuarcy:0.8822270035743713
trainloss:0.14605894272972364 | testloss:17.11624130717246 | accuarcy:0.8865096569061279
trainloss:0.0952077861293219 | testloss:18.13019257079577 | accuarcy:0.8886509537696838
trainloss:0.10391396505292505 | testloss:21.971923857112415 | accuarcy:0.8608136773109436
trainloss:1.155562664323952 | testloss:20.626633802894503 | accuarcy:0.8501070737838745
trainloss:5.643173315562308 | testloss:30.893559396266937 | accuarcy:0.7730192542076111
trainloss:13.735087782144547 | testloss:11.550982251763344 | accuarcy:0.802997887134552
trainloss:5.677116572856903 | testloss:11.846688069403172 | accuarcy:0.8415417671203613
trainloss:3.6993395797908306 | testloss:11.380348352715373 | accuarcy:0.8843683004379272
trainloss:1.7137542960699648 | testloss:14.075968239456415 | accuarcy:0.8865096569061279
trainloss:2.232042054645717 | testloss:20.070361867547035 | accuarcy:0.8436830639839172
trainloss:13.380389118567109 | testloss:12.961846962571144 | accuarcy:0.8179871439933777
trainloss:5.413172818720341 | testloss:13.099523358047009 | accuarcy:0.856531023979187
trainloss:2.0760835595428944 | testloss:13.619954163208604 | accuarcy:0.8886509537696838
trainloss:1.2905899286270142 | testloss:17.72766901552677 | accuarcy:0.856531023979187
trainloss:1.9347536119748838 | testloss:14.906391673721373 | accuarcy:0.8629550337791443
trainloss:2.1229206454008818 | testloss:14.588731775991619 | accuarcy:0.8800856471061707
trainloss:1.4905940552707762 | testloss:19.444260380696505 | accuarcy:0.8629550337791443
trainloss:5.1526844296604395 | testloss:14.73568258434534 | accuarcy:0.8458244204521179
trainloss:2.6978021254763007 | testloss:14.857497323304415 | accuarcy:0.8458244204521179
trainloss:1.6467376677319407 | testloss:13.719625500962138 | accuarcy:0.8800856471061707
trainloss:0.509652393637225 | testloss:14.471574648749083 | accuarcy:0.8843683004379272
trainloss:0.22443032858427614 | testloss:15.903609075117856 | accuarcy:0.8865096569061279
trainloss:0.12529150885529816 | testloss:16.17591433483176 | accuarcy:0.8886509537696838
trainloss:0.08426261390559375 | testloss:17.036522377631627 | accuarcy:0.8843683004379272
trainloss:0.04986236750846729 | testloss:17.46310092919157 | accuarcy:0.8822270035743713
trainloss:0.03949086190550588 | testloss:18.32706015583244 | accuarcy:0.8822270035743713
trainloss:0.027721170423319563 | testloss:18.084734840580495 | accuarcy:0.8843683004379272
trainloss:0.03193701308919117 | testloss:18.249785173364216 | accuarcy:0.8822270035743713
trainloss:0.04952997327200137 | testloss:18.86155753087951 | accuarcy:0.8822270035743713
trainloss:0.19903108023572713 | testloss:17.741519418137614 | accuarcy:0.8779443502426147
trainloss:0.42163144994992763 | testloss:17.63332318724133 | accuarcy:0.8843683004379272
trainloss:2.80683073354885 | testloss:14.008181711193174 | accuarcy:0.8758029937744141
trainloss:5.800614448264241 | testloss:15.929063078016043 | accuarcy:0.7965738773345947
trainloss:3.3747728914022446 | testloss:14.325642494484782 | accuarcy:0.8286938071250916
trainloss:1.8059299909509718 | testloss:12.964236591942608 | accuarcy:0.8800856471061707
trainloss:0.8648910557385534 | testloss:15.525794485583901 | accuarcy:0.8822270035743713
trainloss:0.2412138245999813 | testloss:16.946154106524773 | accuarcy:0.8822270035743713
trainloss:0.13833513640565798 | testloss:18.04287917225156 | accuarcy:0.8886509537696838
trainloss:0.04834642744390294 | testloss:18.93710811290657 | accuarcy:0.8907923102378845
trainloss:0.028744473704136908 | testloss:18.583747401833534 | accuarcy:0.8907923102378845
trainloss:0.021294384088832885 | testloss:18.674494261969812 | accuarcy:0.8907923102378845
trainloss:0.019589923933381215 | testloss:18.590098174929153 | accuarcy:0.8907923102378845
trainloss:0.025503370648948476 | testloss:18.59209606650984 | accuarcy:0.8907923102378845
trainloss:0.03232004534220323 | testloss:18.29904008601443 | accuarcy:0.8865096569061279
trainloss:0.389224894461222 | testloss:17.28253556857817 | accuarcy:0.8865096569061279
trainloss:0.11994107346981764 | testloss:17.3745361957117 | accuarcy:0.8865096569061279
trainloss:0.0487527854857035 | testloss:18.29223274992546 | accuarcy:0.8907923102378845
trainloss:0.024838655081111938 | testloss:18.333647422725335 | accuarcy:0.8907923102378845
trainloss:0.019830706238280982 | testloss:18.385058143205242 | accuarcy:0.8907923102378845
trainloss:0.018348308381973766 | testloss:18.346893462439766 | accuarcy:0.8907923102378845
trainloss:0.018357246764935553 | testloss:18.315342755784513 | accuarcy:0.8907923102378845
trainloss:0.01788114180089906 | testloss:18.207482840371085 | accuarcy:0.8907923102378845
trainloss:0.017496301035862416 | testloss:18.152099956176244 | accuarcy:0.8907923102378845
trainloss:0.01750659689423628 | testloss:18.05285165659734 | accuarcy:0.8907923102378845
trainloss:0.017999552859691903 | testloss:18.133162957441527 | accuarcy:0.8907923102378845
trainloss:0.018910076847532764 | testloss:17.932953940849984 | accuarcy:0.8907923102378845
trainloss:0.019035011500818655 | testloss:17.97708997045993 | accuarcy:0.8907923102378845
trainloss:0.019489527097903192 | testloss:17.946826530009275 | accuarcy:0.8886509537696838
trainloss:0.024145076604327187 | testloss:17.60634887748165 | accuarcy:0.8907923102378845
trainloss:0.020649742160458118 | testloss:17.716980122670066 | accuarcy:0.8907923102378845
trainloss:0.018973197555169463 | testloss:17.817703817243455 | accuarcy:0.8929336071014404
trainloss:0.017863024142570794 | testloss:17.71632861532271 | accuarcy:0.8929336071014404
trainloss:0.0173693163524149 | testloss:17.662800153688295 | accuarcy:0.8907923102378845
trainloss:0.017283508932450786 | testloss:17.7731698936841 | accuarcy:0.8907923102378845
plt.plot(list(range(len(test_acc))), test_acc)
plt.show()
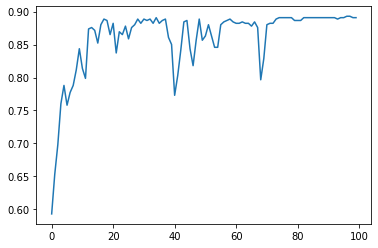
Analysis
We can see that Neural Networks is much powerful for this image recognition task, where a basic neural networks reaches almostly 90% of classification accuracy.
Convolutional Neural Networks¶
Model definition
Define the architecture of model. A very basic convolutional connected neural networks including 2 convolutional layers, 3 linear layers, 4 activation layers, and 1 pooling layers.
Reference: https://pytorch.org/tutorials/beginner/blitz/cifar10_tutorial.html
import torch.nn as nn
import torch.nn.functional as F
class CNet(nn.Module):
def __init__(self):
super().__init__()
self.conv1 = nn.Conv2d(3, 6, 5)
self.pool = nn.MaxPool2d(2, 2)
self.conv2 = nn.Conv2d(6, 16, 5)
self.fc1 = nn.Linear(16 * 5 * 5, 120)
self.fc2 = nn.Linear(120, 100)
self.fc3 = nn.Linear(100, 2)
def forward(self, x):
x = self.pool(F.relu(self.conv1(x)))
x = self.pool(F.relu(self.conv2(x)))
x = torch.flatten(x, 1)
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
cnet = CNet()
train_loss, test_loss, test_acc = train_eval(cnet, conv=True)
trainloss:16.5655797123909 | testloss:16.32100421190262 | accuarcy:0.5952890515327454
trainloss:16.322040677070618 | testloss:16.010993480682373 | accuarcy:0.5952890515327454
trainloss:16.127350330352783 | testloss:15.929425418376923 | accuarcy:0.5952890515327454
trainloss:16.35239452123642 | testloss:15.827909409999847 | accuarcy:0.5952890515327454
trainloss:16.37032687664032 | testloss:16.16121196746826 | accuarcy:0.5952890515327454
trainloss:16.195215940475464 | testloss:15.744493067264557 | accuarcy:0.5952890515327454
trainloss:15.924577534198761 | testloss:15.57081800699234 | accuarcy:0.599571704864502
trainloss:15.660198509693146 | testloss:15.555176556110382 | accuarcy:0.6274089813232422
trainloss:15.40750116109848 | testloss:15.490601539611816 | accuarcy:0.599571704864502
trainloss:15.296328485012054 | testloss:15.193099200725555 | accuarcy:0.6038544178009033
trainloss:14.938752591609955 | testloss:14.573900401592255 | accuarcy:0.6638115644454956
trainloss:15.293941766023636 | testloss:14.694179624319077 | accuarcy:0.6359742879867554
trainloss:14.27346596121788 | testloss:14.26795881986618 | accuarcy:0.6638115644454956
trainloss:13.202391564846039 | testloss:14.026364803314209 | accuarcy:0.6959314942359924
trainloss:13.205775439739227 | testloss:13.359399169683456 | accuarcy:0.7173447608947754
trainloss:11.806512892246246 | testloss:13.617230713367462 | accuarcy:0.7194860577583313
trainloss:10.541242063045502 | testloss:12.536467790603638 | accuarcy:0.762312650680542
trainloss:9.510418385267258 | testloss:12.825072631239891 | accuarcy:0.7858672142028809
trainloss:8.833022490143776 | testloss:11.446995466947556 | accuarcy:0.8115631937980652
trainloss:6.752786178141832 | testloss:14.753793179988861 | accuarcy:0.7580299973487854
trainloss:6.471094459295273 | testloss:12.848074346780777 | accuarcy:0.8137044906616211
trainloss:4.973730765283108 | testloss:12.952815793454647 | accuarcy:0.8543897271156311
trainloss:4.132506957277656 | testloss:13.98931735381484 | accuarcy:0.8286938071250916
trainloss:3.6017012130469084 | testloss:13.47572785243392 | accuarcy:0.8779443502426147
trainloss:2.186511818319559 | testloss:15.169204328209162 | accuarcy:0.8800856471061707
trainloss:1.9312479021027684 | testloss:16.052954833954573 | accuarcy:0.8736616969108582
trainloss:1.2076842077076435 | testloss:19.612629792187363 | accuarcy:0.8693790435791016
trainloss:1.0278319045901299 | testloss:20.19766210578382 | accuarcy:0.8415417671203613
trainloss:2.147738553583622 | testloss:17.987094869371504 | accuarcy:0.856531023979187
trainloss:1.1535658567445353 | testloss:17.071625020354986 | accuarcy:0.8758029937744141
trainloss:1.218346674926579 | testloss:16.95442943740636 | accuarcy:0.8822270035743713
trainloss:0.6150879161432385 | testloss:18.999540204298683 | accuarcy:0.8629550337791443
trainloss:0.2573674552841112 | testloss:20.083426332334056 | accuarcy:0.8758029937744141
trainloss:0.23396171047352254 | testloss:20.305118089308962 | accuarcy:0.8736616969108582
trainloss:0.15180639986647293 | testloss:21.821017378999386 | accuarcy:0.8779443502426147
trainloss:0.15575825492851436 | testloss:20.84359696379397 | accuarcy:0.8779443502426147
trainloss:0.11729160521645099 | testloss:22.08744731504703 | accuarcy:0.8800856471061707
trainloss:0.059096458833664656 | testloss:22.078013686579652 | accuarcy:0.8736616969108582
trainloss:0.04274555156007409 | testloss:22.283621255599428 | accuarcy:0.8693790435791016
trainloss:0.0389849977218546 | testloss:22.58047357527539 | accuarcy:0.8736616969108582
trainloss:0.03718858602223918 | testloss:22.647938015550608 | accuarcy:0.8758029937744141
trainloss:0.03613434545695782 | testloss:22.70252748922212 | accuarcy:0.8715203404426575
trainloss:0.03291765788162593 | testloss:22.804281021439238 | accuarcy:0.8736616969108582
trainloss:0.032353346061427146 | testloss:22.851598072244087 | accuarcy:0.8736616969108582
trainloss:0.030558193364413455 | testloss:23.0214595956204 | accuarcy:0.8715203404426575
trainloss:0.029981693704030477 | testloss:22.951326013513608 | accuarcy:0.8736616969108582
trainloss:0.030101442243903875 | testloss:23.02823777726735 | accuarcy:0.8758029937744141
trainloss:0.02958274004049599 | testloss:22.996343667880865 | accuarcy:0.8693790435791016
trainloss:0.028188446463900618 | testloss:22.957386825612048 | accuarcy:0.8779443502426147
trainloss:0.027906965638976544 | testloss:23.027313708211295 | accuarcy:0.8736616969108582
trainloss:0.02817784098442644 | testloss:23.03236151440069 | accuarcy:0.8715203404426575
trainloss:0.02849870576756075 | testloss:23.006275582301896 | accuarcy:0.8736616969108582
trainloss:0.02923350437777117 | testloss:22.920493953686673 | accuarcy:0.8800856471061707
trainloss:0.02759467376745306 | testloss:22.974577719636727 | accuarcy:0.8779443502426147
trainloss:0.02842437312938273 | testloss:22.923244327423163 | accuarcy:0.8843683004379272
trainloss:0.029553605389082804 | testloss:22.931991453340743 | accuarcy:0.8779443502426147
trainloss:0.027097926737042144 | testloss:22.88842312572524 | accuarcy:0.8822270035743713
trainloss:0.028542573330923915 | testloss:22.857375835999846 | accuarcy:0.8822270035743713
trainloss:0.029436731449095532 | testloss:22.851980926294345 | accuarcy:0.8736616969108582
trainloss:0.026711412705481052 | testloss:22.663545089337276 | accuarcy:0.8779443502426147
trainloss:0.027037274470785633 | testloss:22.691100066993386 | accuarcy:0.8736616969108582
trainloss:0.02839284739457071 | testloss:22.840922350878827 | accuarcy:0.8843683004379272
trainloss:0.027545298915356398 | testloss:22.73120777166332 | accuarcy:0.8800856471061707
trainloss:0.027723617444280535 | testloss:22.753990128287114 | accuarcy:0.8800856471061707
trainloss:0.02819548943080008 | testloss:22.579066053935094 | accuarcy:0.8758029937744141
trainloss:0.02715478913160041 | testloss:22.662728134804638 | accuarcy:0.8779443502426147
trainloss:0.02691403916105628 | testloss:22.587113305693492 | accuarcy:0.8758029937744141
trainloss:0.027195764356292784 | testloss:22.559565913048573 | accuarcy:0.8779443502426147
trainloss:0.027367699396563694 | testloss:22.579832608171273 | accuarcy:0.8736616969108582
trainloss:0.02926202560774982 | testloss:22.78618152171839 | accuarcy:0.8822270035743713
trainloss:0.028241796419024467 | testloss:22.43746130593354 | accuarcy:0.8758029937744141
trainloss:0.02888448699377477 | testloss:22.37507226425805 | accuarcy:0.8758029937744141
trainloss:0.02760410268092528 | testloss:22.418802702450193 | accuarcy:0.8758029937744141
trainloss:0.02757967571960762 | testloss:22.47315842178068 | accuarcy:0.8758029937744141
trainloss:0.02864860204863362 | testloss:22.339538106898544 | accuarcy:0.8779443502426147
trainloss:0.02849567134398967 | testloss:22.439803835004568 | accuarcy:0.8779443502426147
trainloss:0.028708744037430733 | testloss:22.457954928686377 | accuarcy:0.8779443502426147
trainloss:0.027024896116927266 | testloss:22.376477572193835 | accuarcy:0.8779443502426147
trainloss:0.027881928312126547 | testloss:22.259269447415136 | accuarcy:0.8779443502426147
trainloss:0.028295307245571166 | testloss:22.356589737319155 | accuarcy:0.8779443502426147
trainloss:0.03272281639510766 | testloss:22.300489928544266 | accuarcy:0.8779443502426147
trainloss:0.027653078665025532 | testloss:22.247424395522103 | accuarcy:0.8800856471061707
trainloss:0.026844981650356203 | testloss:22.20261083636433 | accuarcy:0.8779443502426147
trainloss:0.027749715896788985 | testloss:22.285310631559696 | accuarcy:0.8779443502426147
trainloss:0.029963435255922377 | testloss:22.115777821658412 | accuarcy:0.8758029937744141
trainloss:0.029530778294429183 | testloss:22.251774420175934 | accuarcy:0.8779443502426147
trainloss:0.029485146573279053 | testloss:22.151881899568252 | accuarcy:0.8779443502426147
trainloss:0.026972459570970386 | testloss:22.189777322259033 | accuarcy:0.8800856471061707
trainloss:0.025048267940292135 | testloss:22.25869986671023 | accuarcy:0.8822270035743713
trainloss:0.02768554142676294 | testloss:22.0718521256058 | accuarcy:0.8800856471061707
trainloss:0.03074320897576399 | testloss:22.077751694014296 | accuarcy:0.8822270035743713
trainloss:0.02789019315969199 | testloss:21.90070634218864 | accuarcy:0.8779443502426147
trainloss:0.026098083042597864 | testloss:22.12703112786403 | accuarcy:0.8822270035743713
trainloss:0.026250310649629682 | testloss:22.126564018893987 | accuarcy:0.8800856471061707
trainloss:0.026967570069245994 | testloss:22.07835976712522 | accuarcy:0.8822270035743713
trainloss:0.027450461057014763 | testloss:21.932137497409713 | accuarcy:0.8779443502426147
trainloss:0.02593959274236113 | testloss:21.89881380085717 | accuarcy:0.8822270035743713
trainloss:0.026251178554957733 | testloss:21.879648564674426 | accuarcy:0.8779443502426147
trainloss:0.030369201907888055 | testloss:22.008912027871702 | accuarcy:0.8800856471061707
trainloss:0.0401928061619401 | testloss:21.919510115520097 | accuarcy:0.8822270035743713
plt.plot(list(range(len(test_acc))), test_acc)
plt.show()
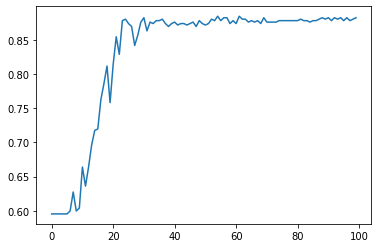
Summary¶
Logistic regression, polynonimal regression and decision tree only achieve \(58.1\%\) accuracy.
Random forest achieve \(65.8\%\) accuracy.
Fully Connected Neural networks achieves \(89.0\%\) accuracy
Convolutional Neural nerworks achieves \(87.8\%\) accuracy
References¶
What is the source of your dataset(s)?
https://www.kaggle.com/datasets/uditsharma72/real-vs-fake-faces
Were any portions of the code or ideas taken from another source? List those sources here and say how they were used.
The idea of Neural Networks is taken from two Deep learing Courses, CS172B & CS178. The knowledge of Image loading and preprocessing is taken from a computer vision course CS116.
List other references that you found helpful.
https://pillow.readthedocs.io/en/stable/reference/Image.html https://docs.scipy.org/doc/scipy/reference/generated/scipy.ndimage.gaussian_filter.html https://pytorch.org/tutorials/beginner/basics/data_tutorial.html https://pytorch.org/tutorials/beginner/blitz/cifar10_tutorial.html
