Key Financial Metrics Analysis of S&P 500 Stocks

Author: Leander von Schönfeld

Email: leander.von.schoenfeld@studium.uni-hamburg.de

LinkedIn: https://www.linkedin.com/in/leander-von-schoenfeld/

Course Project, UC Irvine, Math 10, F22

Introduction

With this project I want to analyze different properties of the S&P 500 stock index using stock data from the last 12 years and current valuation multiples. The main topics will be to evaluate whether you can classify the sector of a stock using key financial metrics, to predict the five year movement of a stock using valuation multiples and vice versa and a small time series analysis predicting stock prices of stocks from the utilities sector.

Loading our datasets and cleaning them up

import pandas as pd
pd.options.mode.chained_assignment = None  # default='warn'
import seaborn as sns
import altair as alt
import numpy as np

First we import our datasets and get a feeling for the data by looking at their first rows.

prices=pd.read_csv("sp500_stocks.csv")
prices.head()

	Date	Symbol	Adj Close	Close	High	Low	Open	Volume
0	2010-01-04	MMM	59.318886	83.019997	83.449997	82.669998	83.089996	3043700.0
1	2010-01-05	MMM	58.947342	82.500000	83.230003	81.699997	82.800003	2847000.0
2	2010-01-06	MMM	59.783295	83.669998	84.599998	83.510002	83.879997	5268500.0
3	2010-01-07	MMM	59.826176	83.730003	83.760002	82.120003	83.320000	4470100.0
4	2010-01-08	MMM	60.247749	84.320000	84.320000	83.300003	83.690002	3405800.0

multiples=pd.read_csv("financials.csv")
multiples.head()

	Symbol	Name	Sector	Price	Price/Earnings	Dividend Yield	Earnings/Share	52 Week Low	52 Week High	Market Cap	EBITDA	Price/Sales	Price/Book	SEC Filings
0	MMM	3M Company	Industrials	222.89	24.31	2.332862	7.92	259.77	175.490	1.387211e+11	9.048000e+09	4.390271	11.34	http://www.sec.gov/cgi-bin/browse-edgar?action...
1	AOS	A.O. Smith Corp	Industrials	60.24	27.76	1.147959	1.70	68.39	48.925	1.078342e+10	6.010000e+08	3.575483	6.35	http://www.sec.gov/cgi-bin/browse-edgar?action...
2	ABT	Abbott Laboratories	Health Care	56.27	22.51	1.908982	0.26	64.60	42.280	1.021210e+11	5.744000e+09	3.740480	3.19	http://www.sec.gov/cgi-bin/browse-edgar?action...
3	ABBV	AbbVie Inc.	Health Care	108.48	19.41	2.499560	3.29	125.86	60.050	1.813863e+11	1.031000e+10	6.291571	26.14	http://www.sec.gov/cgi-bin/browse-edgar?action...
4	ACN	Accenture plc	Information Technology	150.51	25.47	1.714470	5.44	162.60	114.820	9.876586e+10	5.643228e+09	2.604117	10.62	http://www.sec.gov/cgi-bin/browse-edgar?action...

We want to find all companies, where the data is incomplete, and get rid of these companies in our dataset.

miss_val=multiples[multiples.isna().any(axis=1)]["Symbol"]
miss_val

55     ARNC
199      FL
225     HCA
292     MRO
346     OXY
358     PEP
360    PRGO
430     TPR
450     TDG
460     UNP
Name: Symbol, dtype: object

multiples_true = multiples.dropna()
multiples_true

	Symbol	Name	Sector	Price	Price/Earnings	Dividend Yield	Earnings/Share	52 Week Low	52 Week High	Market Cap	EBITDA	Price/Sales	Price/Book	SEC Filings
0	MMM	3M Company	Industrials	222.89	24.31	2.332862	7.92	259.77	175.490	1.387211e+11	9.048000e+09	4.390271	11.34	http://www.sec.gov/cgi-bin/browse-edgar?action...
1	AOS	A.O. Smith Corp	Industrials	60.24	27.76	1.147959	1.70	68.39	48.925	1.078342e+10	6.010000e+08	3.575483	6.35	http://www.sec.gov/cgi-bin/browse-edgar?action...
2	ABT	Abbott Laboratories	Health Care	56.27	22.51	1.908982	0.26	64.60	42.280	1.021210e+11	5.744000e+09	3.740480	3.19	http://www.sec.gov/cgi-bin/browse-edgar?action...
3	ABBV	AbbVie Inc.	Health Care	108.48	19.41	2.499560	3.29	125.86	60.050	1.813863e+11	1.031000e+10	6.291571	26.14	http://www.sec.gov/cgi-bin/browse-edgar?action...
4	ACN	Accenture plc	Information Technology	150.51	25.47	1.714470	5.44	162.60	114.820	9.876586e+10	5.643228e+09	2.604117	10.62	http://www.sec.gov/cgi-bin/browse-edgar?action...
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
500	XYL	Xylem Inc.	Industrials	70.24	30.94	1.170079	1.83	76.81	46.860	1.291502e+10	7.220000e+08	2.726209	5.31	http://www.sec.gov/cgi-bin/browse-edgar?action...
501	YUM	Yum! Brands Inc	Consumer Discretionary	76.30	27.25	1.797080	4.07	86.93	62.850	2.700330e+10	2.289000e+09	6.313636	212.08	http://www.sec.gov/cgi-bin/browse-edgar?action...
502	ZBH	Zimmer Biomet Holdings	Health Care	115.53	14.32	0.794834	9.01	133.49	108.170	2.445470e+10	2.007400e+09	3.164895	2.39	http://www.sec.gov/cgi-bin/browse-edgar?action...
503	ZION	Zions Bancorp	Financials	50.71	17.73	1.480933	2.60	55.61	38.430	1.067068e+10	0.000000e+00	3.794579	1.42	http://www.sec.gov/cgi-bin/browse-edgar?action...
504	ZTS	Zoetis	Health Care	71.51	32.80	0.682372	1.65	80.13	52.000	3.599111e+10	1.734000e+09	9.280896	18.09	http://www.sec.gov/cgi-bin/browse-edgar?action...

495 rows × 14 columns

len(miss_val)==len(multiples)-len(multiples_true)

True

As we see there are 10 companies with missing data. We check that dropna works correctly, by seeing if the number of rows in our new dataframe are the same.

Next we only focus on Adjusted Closing Dates in our prices dataset because we look for longterm trends and in the difference between the adjusted closing price and the other prices is quite small on average. Therefore we drop all other rows.

prices_adj = prices.drop(["Close", "High", "Low", "Open", "Volume"], axis=1).dropna()
prices_adj.head()

	Date	Symbol	Adj Close
0	2010-01-04	MMM	59.318886
1	2010-01-05	MMM	58.947342
2	2010-01-06	MMM	59.783295
3	2010-01-07	MMM	59.826176
4	2010-01-08	MMM	60.247749

Next we want to get rid of all stocks, where some of the data about the financial statements is missing and therefore drop these rows.

prices_true=prices_adj[~prices_adj["Symbol"].isin(miss_val)]
prices_true

	Date	Symbol	Adj Close
0	2010-01-04	MMM	59.318886
1	2010-01-05	MMM	58.947342
2	2010-01-06	MMM	59.783295
3	2010-01-07	MMM	59.826176
4	2010-01-08	MMM	60.247749
...	...	...	...
1633739	2022-11-18	ZTS	145.639999
1633740	2022-11-21	ZTS	147.330002
1633741	2022-11-22	ZTS	148.630005
1633742	2022-11-23	ZTS	150.470001
1633743	2022-11-25	ZTS	150.100006

1542379 rows × 3 columns

Plotting the S&P 500 index normed at year 2010

We want to get a feeling for how the S&P 500 developed over the years, using just our data. We add a year column but also put the symbol into the year column so that we can still match the data of the respective stocks together.

prices_sectors = prices_true.copy()
prices_sectors["Year"] = prices_sectors.Date.str[0:4]+ ' ' + prices_sectors['Symbol']
prices_sectors.head()

	Date	Symbol	Adj Close	Year
0	2010-01-04	MMM	59.318886	2010 MMM
1	2010-01-05	MMM	58.947342	2010 MMM
2	2010-01-06	MMM	59.783295	2010 MMM
3	2010-01-07	MMM	59.826176	2010 MMM
4	2010-01-08	MMM	60.247749	2010 MMM

To see an overall trend we use the first stock price of every stock and every year.

prices_sectors.drop_duplicates(subset ='Year', keep ='first', inplace =True)
prices_sectors.drop(["Date"],axis=1,inplace=True)
prices_sectors

	Symbol	Adj Close	Year
0	MMM	59.318886	2010 MMM
252	MMM	63.603325	2011 MMM
504	MMM	62.773624	2012 MMM
754	MMM	73.182358	2013 MMM
1006	MMM	109.054214	2014 MMM
...	...	...	...
1632509	ZTS	69.990440	2018 ZTS
1632760	ZTS	82.876381	2019 ZTS
1633012	ZTS	132.432312	2020 ZTS
1633265	ZTS	162.432663	2021 ZTS
1633517	ZTS	233.654770	2022 ZTS

6203 rows × 3 columns

Assume one stock is priced at 5 dollars per share and one stock is priced at 10 dollars per share but their market cap is equal. If we would just add all stock prices, the stock with less outstanding shares and a higher share price is weighted more in the calculation. Therefore we scale all stock prices to 100 for their first year in the S&P 500 to get a good feeling on how the S&P 500 developed over the last decade.

ser = prices_sectors.groupby("Symbol").first()["Adj Close"]
prices_sectors["temp"] = prices_sectors["Symbol"].map(lambda abb: ser[abb])
prices_sectors["Adj Close Norm"]=100*prices_sectors["Adj Close"]/prices_sectors["temp"]
prices_sectors.drop(["temp"],axis=1,inplace=True)
prices_sectors

	Symbol	Adj Close	Year	Adj Close Norm
0	MMM	59.318886	2010 MMM	100.000000
252	MMM	63.603325	2011 MMM	107.222723
504	MMM	62.773624	2012 MMM	105.824011
754	MMM	73.182358	2013 MMM	123.371093
1006	MMM	109.054214	2014 MMM	183.844003
...	...	...	...	...
1632509	ZTS	69.990440	2018 ZTS	240.943436
1632760	ZTS	82.876381	2019 ZTS	285.303534
1633012	ZTS	132.432312	2020 ZTS	455.900779
1633265	ZTS	162.432663	2021 ZTS	559.177564
1633517	ZTS	233.654770	2022 ZTS	804.361036

6203 rows × 4 columns

f = lambda x: sum(prices_sectors["Adj Close Norm"][pd.to_numeric(prices_sectors["Year"].str[:4])==x])

g = lambda x: len(prices_sectors["Adj Close Norm"][pd.to_numeric(prices_sectors["Year"].str[:4])==x])

overall = [f(x)/g(x) for x in range(2010,2023)]
overall

[100.0,
 125.71174470297127,
 130.7469567085745,
 160.9021856202607,
 218.2566878000859,
 260.9022058217084,
 273.15436050027466,
 315.22020155526695,
 397.4428705257547,
 382.09487113487626,
 514.897322817739,
 654.9769290679288,
 867.8759189597679]

sp500 = pd.DataFrame()
sp500["Year"]=range(2010,2023)
sp500["Score"]=overall
sp500

	Year	Score
0	2010	100.000000
1	2011	125.711745
2	2012	130.746957
3	2013	160.902186
4	2014	218.256688
5	2015	260.902206
6	2016	273.154361
7	2017	315.220202
8	2018	397.442871
9	2019	382.094871
10	2020	514.897323
11	2021	654.976929
12	2022	867.875919

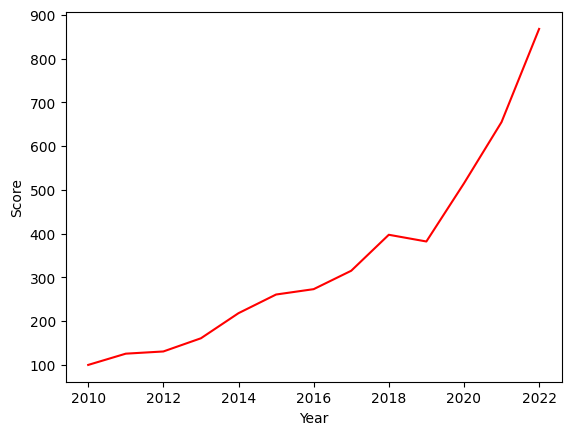
Using a seaborn plot, we see that the overall trend was very positive. But some market movements are not included in the chart because only yearly data is used (e.g. a bear market in early 2020 because of the Covid 19 pandemic). However the goal of the chart was to get an overall feeling.

sns.lineplot(data=sp500, x="Year", y="Score", color="red")

<AxesSubplot: xlabel='Year', ylabel='Score'>

Merging our datasets

Now we want to merge our two datasets multiples_true and prices_sectors. We us the pivot method to do so. Also we get rid of the Adj Close Norm column and just use the adjusted closing prices. Reference 1 Reference 2

mr = prices_sectors.copy()
realyear=[i[:4] for i in mr["Year"]]
mr["Real Year"]=realyear
mr.head()

	Symbol	Adj Close	Year	Adj Close Norm	Real Year
0	MMM	59.318886	2010 MMM	100.000000	2010
252	MMM	63.603325	2011 MMM	107.222723	2011
504	MMM	62.773624	2012 MMM	105.824011	2012
754	MMM	73.182358	2013 MMM	123.371093	2013
1006	MMM	109.054214	2014 MMM	183.844003	2014

mr=mr.pivot(index="Symbol",
         columns="Real Year",
         values= "Adj Close")

mr.head()

Real Year	2010	2011	2012	2013	2014	2015	2016	2017	2018	2019	2020	2021	2022
Symbol
A	20.434929	27.342327	23.816809	27.615749	37.446896	38.134743	38.664230	44.659348	65.523422	64.262276	84.799675	118.001701	156.479996
AAL	4.496876	10.040195	4.826837	13.179525	23.907927	51.079918	39.095455	44.741226	51.647556	31.963160	28.982893	15.130000	18.750000
AAP	38.432693	62.621048	66.313416	69.793709	105.951363	153.358200	147.469162	165.506012	103.141106	153.790192	155.478271	154.917297	236.779999
AAPL	6.572423	10.121366	12.629211	17.010893	17.568449	24.819241	24.323219	27.413372	41.310070	38.439735	74.207466	128.997803	182.009995
ABBV	NaN	NaN	NaN	23.636871	36.381527	47.606876	42.991688	48.374146	79.061188	74.481514	80.137360	99.552361	134.029205

df = pd.merge(multiples_true, mr, on='Symbol')
df = df.sort_values(by=['Symbol'])
df.drop(["Price","52 Week Low", "52 Week High"],axis=1, inplace=True)
df.head()

	Symbol	Name	Sector	Price/Earnings	Dividend Yield	Earnings/Share	Market Cap	EBITDA	Price/Sales	Price/Book	...	2013	2014	2015	2016	2017	2018	2019	2020	2021	2022
11	A	Agilent Technologies Inc	Health Care	27.45	0.875698	2.10	2.198461e+10	1.094000e+09	6.493563	4.56	...	27.615749	37.446896	38.134743	38.664230	44.659348	65.523422	64.262276	84.799675	118.001701	156.479996
26	AAL	American Airlines Group	Industrials	9.92	0.778210	3.91	2.459485e+10	5.761000e+09	0.580226	6.03	...	13.179525	23.907927	51.079918	39.095455	44.741226	51.647556	31.963160	28.982893	15.130000	18.750000
7	AAP	Advance Auto Parts	Consumer Discretionary	19.54	0.218321	6.19	8.123612e+09	8.539410e+08	1.130106	2.51	...	69.793709	105.951363	153.358200	147.469162	165.506012	103.141106	153.790192	155.478271	154.917297	236.779999
41	AAPL	Apple Inc.	Information Technology	16.86	1.579541	9.20	8.095080e+11	7.938600e+10	3.458609	5.66	...	17.010893	17.568449	24.819241	24.323219	27.413372	41.310070	38.439735	74.207466	128.997803	182.009995
3	ABBV	AbbVie Inc.	Health Care	19.41	2.499560	3.29	1.813863e+11	1.031000e+10	6.291571	26.14	...	23.636871	36.381527	47.606876	42.991688	48.374146	79.061188	74.481514	80.137360	99.552361	134.029205

5 rows × 24 columns

Classifying stocks using the K-Means method

The first thing we want to do is, to see if we can predict, whether the sector of a stock is Real Estate, Industrials or Utilities, using the Price/Sales and the Dividend Yield multiple with the K-Means method. Reference

First let us have a look on how our data looks:

df2= df[df['Sector'].eq("Real Estate") | df['Sector'].eq("Utilities") | df['Sector'].eq("Industrials")]

brush = alt.selection_interval(encodings=["x","y"])

i1 = alt.Chart(df2).mark_circle().encode(
    x="Price/Sales",
    y="Dividend Yield",
    color=alt.condition(brush, "Sector:N", alt.value("green"))
).add_selection(brush) 

i2 = alt.Chart(df2).mark_bar().encode(
    x="Sector:N",
    y=alt.Y("count()", scale=alt.Scale(domain=[0,55])),
    color="Sector:N"
).transform_filter(brush)

alt.hconcat(i1,i2)

When looking at the data and creating a brush, we clearly see, that there is at least some sort of characteristic properties for stocks from each sector. Industrials tend to have a low dividend yield and a low Price/Sales multiple, Utilities also have a low Price/Sales multiple, but their dividend yield is higher on average and Real Estate stocks have a high Price/Sales multiple. We want to use different machine learning techniques to see, how well these methods can classify given stocks.

First we use the K-Means method. We don’t initialize centroids.

from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=3, max_iter=10, n_init=5, random_state=2)
kmeans.fit(df2[["Dividend Yield","Price/Sales"]])
kmeans.predict(df2[["Dividend Yield","Price/Sales"]])

array([0, 2, 2, 2, 0, 0, 0, 1, 0, 1, 1, 2, 0, 2, 0, 1, 0, 0, 2, 2, 0, 0,
       2, 0, 0, 1, 0, 2, 2, 2, 0, 2, 2, 1, 1, 2, 1, 0, 2, 2, 0, 1, 2, 0,
       0, 2, 1, 0, 0, 0, 0, 0, 0, 2, 0, 2, 0, 0, 0, 2, 0, 2, 0, 2, 0, 2,
       2, 2, 0, 0, 0, 1, 0, 0, 2, 0, 1, 0, 2, 2, 1, 0, 1, 0, 0, 0, 0, 1,
       2, 1, 2, 0, 0, 1, 0, 0, 2, 1, 2, 2, 0, 2, 2, 0], dtype=int32)

cluster = kmeans.predict(df2[["Dividend Yield","Price/Sales"]])

Now we want to test whether our results from the prediction using K-Means are actually correct. We use a dictionary and list comprehension to do so. Reference

mapping = {0:'Industrials', 1:'Real Estate', 2:'Utilities'}
df2["temp"] = [mapping[i] for i in cluster]
df2["prediction"]=df2["Sector"]==df2["temp"]

Let’s do a chart that shows how well the K-Means algorithm performed.

c2 = alt.Chart(df2).mark_circle().encode(
    x="Price/Sales",
    y="Dividend Yield",
    color="prediction:N"
)
c2

We see, the algorithm worked quite well. To evaluate how good it worked, we can do the following calculation:

len(df2[df2["prediction"]])/len(df2)

0.8653846153846154

The algorithm predicted 86.5% of the stocks correctly. Let’s see if a decision tree works better and how we can avoid overfitting.

Classifying stocks using decision trees

from sklearn.model_selection import train_test_split
X = df2[["Price/Sales","Dividend Yield"]]
y = df2["Sector"]
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.9, random_state=0)

from sklearn.tree import DecisionTreeClassifier
clf = DecisionTreeClassifier(max_leaf_nodes=5)
clf.fit(X_train,y_train)

DecisionTreeClassifier(max_leaf_nodes=5)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

clf.score(X_train,y_train)

0.9247311827956989

clf.score(X_test, y_test)

0.8181818181818182

Using max_leaf_nodes=5, the performance on our test set is much worse than on the training set (more than 10 percentage points difference) and also worse than with the K_Means method. To see, which max_leaf_nodes value between 2 and 10 gives us the best score on the test set we use a for-loop. Reference

mlf_candidates = range(2,10)
scores = dict()
train_scores=dict()
for i in mlf_candidates:
    clf = DecisionTreeClassifier(max_leaf_nodes=i)
    clf.fit(X_train,y_train)
    scores[i] = clf.score(X_test,y_test)
    train_scores[i] = clf.score(X_train,y_train)
print(scores)
print(train_scores)

{2: 0.5454545454545454, 3: 0.8181818181818182, 4: 0.8181818181818182, 5: 0.8181818181818182, 6: 0.8181818181818182, 7: 0.9090909090909091, 8: 0.9090909090909091, 9: 0.9090909090909091}
{2: 0.6989247311827957, 3: 0.8709677419354839, 4: 0.9247311827956989, 5: 0.9247311827956989, 6: 0.946236559139785, 7: 0.956989247311828, 8: 0.956989247311828, 9: 0.967741935483871}

pd.Series(scores).idxmax()

7

scores[7]

0.9090909090909091

The best possibility for max_leaf_nodes seems to be 7. Let’s check overfitting:

clf7 = DecisionTreeClassifier(max_leaf_nodes=5)
clf7.fit(X_train,y_train)
clf.score(X_train,y_train)

0.967741935483871

We see that it is now overfitting way less than before. But there is still a difference of more than 6 percentage points.

Now let’s plot the decision tree with max_leaf_nodes=7:

import matplotlib.pyplot as plt
from sklearn.tree import plot_tree

fig = plt.figure(figsize=(20,10))
_ = plot_tree(clf7, 
                   feature_names=clf7.feature_names_in_,
                   class_names=clf7.classes_,
                   filled=True)

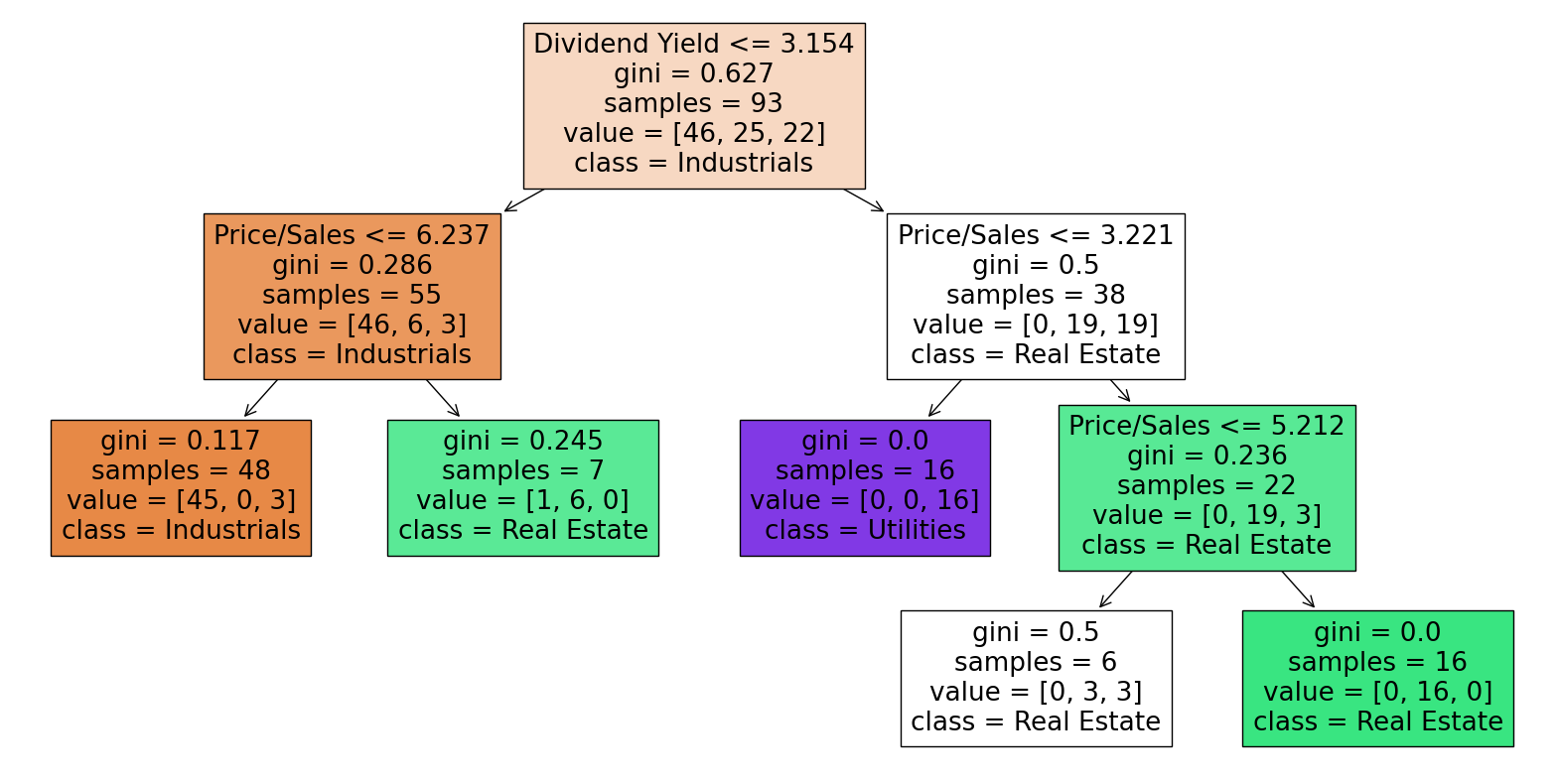
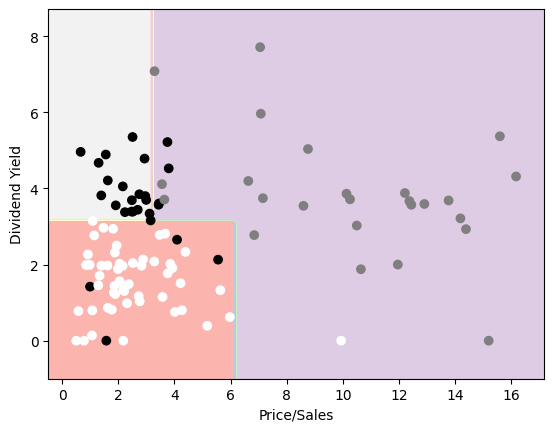
Next let’s make a chart of the results of our decision tree, which we will do by coloring the different decison areas in different colors using the DecisionBoundaryDisplay method. Reference

In order to get a proper coloring for our plot we need to use a similar trick with a dictionary before and afterwards we see the stocks and decision areas. I did not know how to get a legend for the colors of the scatterplot, because of the trick I used, but white stands for Industrials, black stands for Utilites and grey for Real Estate.

from sklearn.inspection import DecisionBoundaryDisplay 
import plotly.express as px

mapp = {'Industrials':0, 'Real Estate':1, 'Utilities':2}
df2["temp2"] = [mapp[i] for i in df2["Sector"]]

x=df2["Price/Sales"]
y=df2["Dividend Yield"]
z=df2["temp2"]

DecisionBoundaryDisplay.from_estimator(
        clf7,
        X,
        cmap='Pastel1'
    )
plt.scatter(x,y,c=z,cmap='binary')

<matplotlib.collections.PathCollection at 0x7fb0b89667a0>

Linear Regression to predict the Price/Earnings multiple

The second central project is to look how the Price/Earnings multiple is influenced by current movements in the stock market.

First we add a new column to our dataframe which gives a multiple for the development of every stock over the last five years.

df["fy_move"]=df['2022']/df['2017']

Now we want to restrict the Price/Earnings multiple to the most common area between zero and fifty, as if we would take all values into account, the impact of the outliers would be to large. This makes sense, as a P/E ratio outside of that range would imply a very unusual economic situation of the company.

df['P/E']=df['Price/Earnings'][(df['Price/Earnings']>0) & (df['Price/Earnings']<50)]

By looking at the chart we see that there is a positive correlation between the P/E multiple and the movement over the last five years. This was what I expected, as a positive movement in the last five years increases the price of the stock and if we assume a symmetric distribution around zero for the development of earnings, on average the Price/Earnings multiple will go up.

alt.Chart(df).mark_circle().encode(
    x=alt.X("fy_move", axis=alt.Axis(format='00%', title='Five Year Movement')),
    y=alt.Y("P/E", axis=alt.Axis(title='Price/Earnings Multiple'))
)

Now let’s check these results by using a linear regression. Note: The results can be only taken into account for usual P/E ratios between zero and fifty.

from sklearn.linear_model import LinearRegression

regr = LinearRegression(fit_intercept=True)

data = {'P/E': df['P/E'],
        'fy_move': df['fy_move']
        }

df_mini = pd.DataFrame(data).dropna()
df_mini.shape
df_mini.head()

	P/E	fy_move
11	27.45	3.503858
26	9.92	0.419077
7	19.54	1.430643
41	16.86	6.639460
3	19.41	2.770679

regr.fit(df_mini[["fy_move"]],df_mini["P/E"]).coef_

array([2.25662875])

We see that if a stock has increased its price a hundred percentage points more in the last five years, it’s P/E multiple is predicted to be 2.26 points higher.

df_mini['P/E_pred'] = regr.predict(df_mini[['fy_move']])

c4 = alt.Chart(df_mini).mark_circle().encode(
    x=alt.X("fy_move", axis=alt.Axis(format='00%', title='Five Year Movement')),
    y=alt.Y("P/E", axis=alt.Axis(title='Price/Earnings Multiple'))
)

c5 = alt.Chart(df_mini).mark_line(color="black", size=3).encode(
    x="fy_move",
    y="P/E_pred"
)

c4+c5

The line graph shows us the predicted values for our P/E multiple based on the performance of a stock in the last five years.

r_squared1 = regr.score(df_mini[["fy_move"]],df_mini["P/E"])
f'The R^2 value of our regression is {r_squared1}'

'The R^2 value of our regression is 0.10920701719531833'

Only around 7 percent of the P/E multiple is explained by the five year movement. So we try to add another variable. But to let it make sense, we now predict the five year movement based on two other multiples.

Multivariate Regression to predict the Five Year Movement

We also calculate the Market Cap/EBITDA multiple. To make that multiple financially correct, we should use Enterprise Value instead of Market Cap (Equity Value), but as these values can’t be derived from our data we use this multiple instead and restrict it to the usual values between zero and thirty.

df_mini["M"]=df["Market Cap"]/df["EBITDA"]

df_mini["M"]=df_mini["M"][(df_mini["M"]>0)&(df_mini["M"]<30)]
df_mini=df_mini.dropna()

We want to do a multivariable regression using the P/E multiple and the Market Cap/EBITDA multiple and do a three dimensional plot of the results.

reg = LinearRegression(fit_intercept=True)

reg.fit(df_mini[["M","P/E"]],df_mini["fy_move"])

LinearRegression()

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

df_mini['fy_pred'] = reg.predict(df_mini[["M","P/E"]])

r_squared = reg.score(df_mini[["M","P/E"]],df_mini["fy_move"])
f'The R^2 value of our regression is {r_squared}'

'The R^2 value of our regression is 0.1318268964774878'

The R^2 value shows us that only 13% of the the five year movement can be explained by our two multiple. So in general their doesn’t seem to be a big linear correlation between our chosen variables. But at least our model is now twice as good as our first linear regression.

We try this using Matplotlib to plot the stocks and the prediction surface for the five year movement based on the Market Cap/EBITDA and the Price/Earnings multiples and our result is correct, but as we need to plot our graph in three dimensions, it is impossible to actually see the relevant information from this plot. Reference 1 Reference 2

fig = plt.figure()
ax = plt.axes(projection='3d')
ax.scatter3D(df_mini['M'],df_mini['P/E'],df_mini['fy_move'])
ax.set_xlabel('Market Cap/EBITDA')
ax.set_ylabel('Price/Earnings')
ax.set_zlabel('Five Year Movement')
ax.plot_trisurf(df_mini['M'],df_mini['P/E'],df_mini['fy_pred'])

<mpl_toolkits.mplot3d.art3d.Poly3DCollection at 0x7fb0ad9e4670>

Therefore I decided to use the plotly.grap_objects library which enables to do really nice and informative three-dimensional interactive charts. Reference

from scipy.interpolate import griddata
import plotly.graph_objects as go


x = np.array(df_mini['M'])
y = np.array(df_mini['P/E'])
z = np.array(df_mini['fy_pred'])
a = np.array(df_mini['fy_move'])


xi = np.linspace(x.min(), x.max(), 100)
yi = np.linspace(y.min(), y.max(), 100)

X,Y = np.meshgrid(xi,yi)

Z = griddata((x,y),z,(X,Y), method='cubic')
A = griddata((x,y),a,(X,Y), method='cubic')

layout = go.Layout(
    margin=dict(l=80, r=80, t=100, b=80),scene= dict(
        xaxis_title='Market Cap/EBITDA',
        yaxis_title='Price/Earnings',
        zaxis_title='Five Year Movement'
    ))


fig = go.Figure(go.Surface(x=xi,y=yi,z=Z), layout=layout)
fig.add_scatter3d(x=X.flatten(), y=Y.flatten(), z = A. flatten(), mode='markers', 
                  marker=dict(size=2, color=A.flatten(),               
                              colorscale='darkmint'))
fig.show()

The color of the surface corresponds to the predicted five year movement and the legend for the colors is on the right side of the plot. Every point corresponds to a stock and shows the empirical five year movement of the respective stock. A darker green of a point symbolizes a higher five year movement of the corresponding stock. When going with the mouse over points you also see the values for the different axis.

From the surface we see, that the predicted five year movement is going up, when both multiples have higher values (positive correlation).

Stock Price Prediction

The last thing we wanna do in this project is to use a RandomForestRegressor to predict the 2022 stock prices of Utilities companies based on the five years before (2017,2022). Reference

First we create a new dataframe consisting of the necessary data and make numpy arrays to use our RandomForestRegressor:

dfu = df[df['Sector']=="Utilities"]

from sklearn.ensemble import RandomForestRegressor

x1,x2,x3,x4,x5,y=dfu["2017"],dfu["2018"],dfu["2019"],dfu["2020"],dfu["2021"],dfu["2022"]

x1,x2,x3,x4,x5=np.array(x1).reshape(-1,1),np.array(x2).reshape(-1,1),np.array(x3).reshape(-1,1),np.array(x4).reshape(-1,1),np.array(x5).reshape(-1,1)

x=np.concatenate((x1,x2,x3,x4,x5),axis=1)

We instantiate such a regressor, split our data and then fit the training data and predict the test data.

model=RandomForestRegressor(n_estimators=100, max_features=5, random_state=0)

X1_train,X1_test,y1_train,y1_test = train_test_split(x, y, train_size=0.9, random_state=0)

model.fit(X1_train,y1_train)

RandomForestRegressor(max_features=5, random_state=0)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

prediction = model.predict(X1_test)

In order to get a good plot, we need to get a dataframe, where we have columns with the actual data of the stocks in the testset and the predicted data in other columns.

df4=pd.DataFrame(X1_test)
df5=pd.DataFrame(prediction)
df6=pd.concat([df4,df5],axis=1)
df7=pd.DataFrame(y1_test.values)
df8=pd.concat([df4,df7],axis=1)

df_plot=pd.concat([df6,df8],axis=0).transpose()
df_plot["Year"]=range(2017,2023)
df_plot.columns = ["Prediction1","Prediction2","Prediction3","Actual1","Actual2","Actual3","Year"]
df_plot

	Prediction1	Prediction2	Prediction3	Actual1	Actual2	Actual3	Year
0	9.617868	86.187241	24.832394	9.617868	86.187241	24.832394	2017
1	9.477143	92.480362	25.914534	9.477143	92.480362	25.914534	2018
2	12.860688	96.775284	32.189873	12.860688	96.775284	32.189873	2019
3	18.765497	139.030411	43.180630	18.765497	139.030411	43.180630	2020
4	22.521595	119.689957	28.016165	22.521595	119.689957	28.016165	2021
0	29.926051	143.434947	41.327859	24.206093	131.990005	40.862453	2022

We see that there are three stocks in our testset. We want to plot the actual stock prices for these three stocks in red and the predicted stock data in blue. Reference

base = alt.Chart(df_plot.reset_index()).encode(x=alt.X('Year',scale=alt.Scale(domain=(2017,2022)), axis=alt.Axis(format='', title='Year')))
alt.layer(
    base.mark_line(color='blue').encode(y=alt.Y('Prediction1',axis=alt.Axis(title='Price'))),
    base.mark_line(color='red').encode(y='Actual1'),
    base.mark_line(color='blue').encode(y='Prediction2'),
    base.mark_line(color='red').encode(y='Actual2'),
    base.mark_line(color='blue').encode(y='Prediction3'),
    base.mark_line(color='red').encode(y='Actual3')
).interactive()

As we can see, the accuracy of RandomForestRegressor was quite different. The best result is achieved for the second stock, where you have to zoom in to see a difference between the red and the blue line. But I would say the overall result is quite good. Whether a stock went up or down was predicted right for all three stocks, eventhough two of them dropped in price the year before.

Summary

To summarize we can say that both the K-Means algorithm and Decision Trees work quite well when it comes to classifying stocks by their sector. Using the optimal number for max_leaf_nodes, we get a slightly better result using Decision trees, but the difference is only four percentage points. We also saw a small correlation between the past movement of a stock and some of the key financial metrics. Actually I expected an even bigger correaltion and was quite surprised by the low R^2 scores of the regressions. When using a RandomForestRegressor to analyze stock price movements, we can get at least an idea into which direction the stock price will move next. How well our time series analysis predicted future stock prices was very different for different stocks.

References

Your code above should include references. Here is some additional space for references.

• What is the source of your dataset(s)?

https://github.com/datasets/s-and-p-500-companies-financials/blob/master/data/constituents-financials.csv https://www.kaggle.com/datasets/andrewmvd/sp-500-stocks/code

Full list of references including further sites helping with general ideas:

https://jakevdp.github.io/PythonDataScienceHandbook/03.07-merge-and-join.html https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.concat.html https://stackoverflow.com/questions/21415661/logical-operators-for-boolean-indexing-in-pandas https://www.kaggle.com/questions-and-answers/169669 https://www.kaggle.com/code/kallefischer/sp-500-prediction-67-5-accuracy https://stackoverflow.com/questions/57207108/typeerror-ufunc-isfinite-not-supported-for-the-input-types-and-the-inputs-co https://stackoverflow.com/questions/57481995/how-to-generate-a-3d-triangle-surface-trisurf-plot-in-python-with-matplotlib https://stackoverflow.com/questions/63697847/changing-label-names-of-kmean-clusters https://www.youtube.com/watch?v=BJ6kyj-st9k https://stackoverflow.com/questions/69625661/create-a-3d-surface-plot-in-plotly https://pandas.pydata.org/docs/user_guide/reshaping.html https://matplotlib.org/stable/tutorials/colors/colormaps.html https://scikit-learn.org/stable/auto_examples/tree/plot_iris_dtc.html https://github.com/altair-viz/altair/issues/968

Submission

Using the Share button at the top right, enable Comment privileges for anyone with a link to the project. Then submit that link on Canvas.

Created in Deepnote