Week 7 Videos

Linear data with an outlier

import numpy as np
import matplotlib.pyplot as plt

rng = np.random.default_rng()

type(rng)

numpy.random._generator.Generator

rng.random(5)

array([0.71766176, 0.67084367, 0.3629894 , 0.63571399, 0.2977128 ])

30*rng.random(5) - 20

array([ -4.40385734,  -6.41524188,   1.36656718, -19.49290652,
        -0.85800345])

m,b = 30*rng.random(2) - 20

x = np.arange(0, 10, 0.5)

x

array([0. , 0.5, 1. , 1.5, 2. , 2.5, 3. , 3.5, 4. , 4.5, 5. , 5.5, 6. ,
       6.5, 7. , 7.5, 8. , 8.5, 9. , 9.5])

y = m*x+b

fig, ax = plt.subplots()
ax.scatter(x, y)

<matplotlib.collections.PathCollection at 0x7fa719099a60>

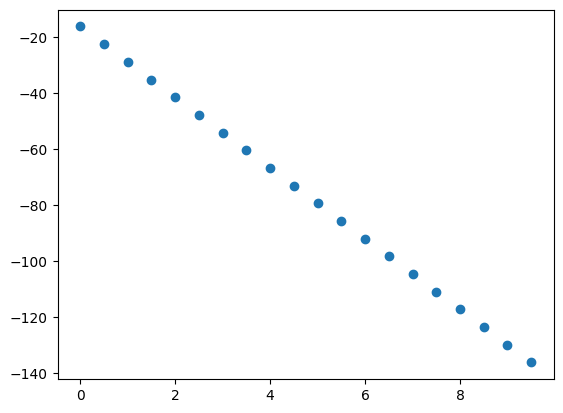
noise = rng.normal(loc=0, scale=10, size=y.shape)

y2 = y+noise

fig, ax = plt.subplots()
ax.scatter(x, y2)

<matplotlib.collections.PathCollection at 0x7fa735291b20>

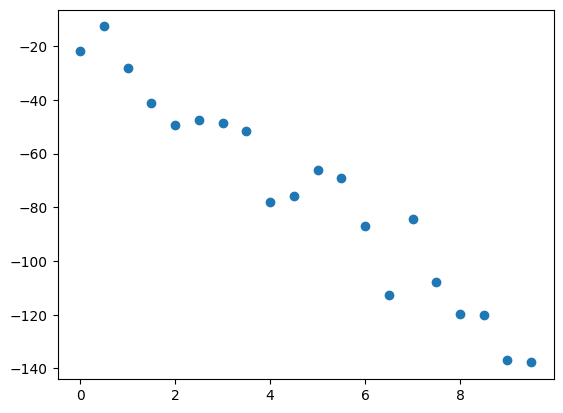
y2[5] = 500

fig, ax = plt.subplots()
ax.scatter(x, y2)

<matplotlib.collections.PathCollection at 0x7fa7359da3a0>

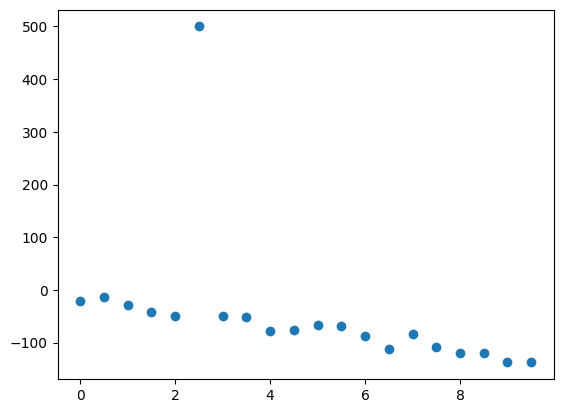
Line of best fit using Mean Squared Error

from sklearn.linear_model import LinearRegression

reg = LinearRegression()

x.shape

(20,)

X = x.reshape(-1,1)

reg.fit(X, y2)

LinearRegression()

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

ypred = reg.predict(X)

fig, ax = plt.subplots()
ax.scatter(x, y2)
ax.plot(x, ypred, 'r')

[<matplotlib.lines.Line2D at 0x7fa717972460>]

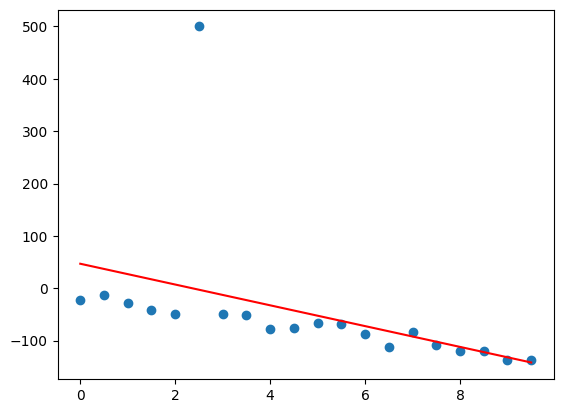
Line of best fit using Mean Absolute Error

Reference: Stack Overflow

from sklearn.linear_model import SGDRegressor

sgdreg = SGDRegressor(loss="epsilon_insensitive", epsilon=0)

sgdreg.fit(X, y2)

SGDRegressor(epsilon=0, loss='epsilon_insensitive')

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

ypred2 = sgdreg.predict(X)

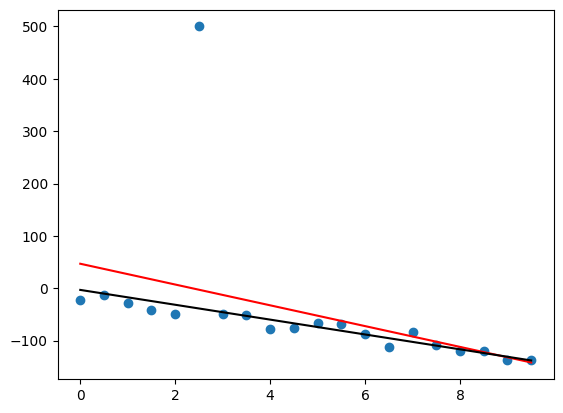
fig, ax = plt.subplots()
ax.scatter(x, y2)
ax.plot(x, ypred, 'r')
ax.plot(x, ypred2, 'k')

[<matplotlib.lines.Line2D at 0x7fa7018b3130>]

Computing Mean Squared Error and Mean Absolute Error in scikit-learn

from sklearn.metrics import mean_absolute_error, mean_squared_error

mean_squared_error(y2, ypred)

13823.74709827255

mean_squared_error(y2, ypred2)

14622.352062657656

mean_absolute_error(y2, ypred)

51.65405629230766

mean_absolute_error(y2, ypred2)

35.41119321144292

((y2-ypred)**2).mean()

13823.74709827255

((y2-ypred)**2).sum()/len(y2)

13823.74709827255

(abs(y2-ypred)).mean()

51.65405629230766

Created in Deepnote